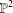Refine search
Actions for selected content:
5 results
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in ℂ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 69 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 06 October 2025, pp. 388-420
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A support theorem for Hilbert schemes of planar curves, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 28 April 2021, pp. 835-882
- Print publication:
- April 2021
-
- Article
- Export citation
The integral cohomology of the Hilbert scheme of points on a surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e40
-
- Article
-
- You have access
- Open access
- Export citation
ON THE POSITION OF NODES OF PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 62-68
- Print publication:
- February 2021
-
- Article
-
- You have access
- Export citation
Higher Nash blowups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1493-1510
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation