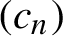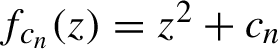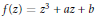Refine search
Actions for selected content:
10 results
A solution to the degree-d twisted rabbit problem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 06 August 2025, pp. 3490-3505
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A flower theorem in dimension two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 3223-3254
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Selected Topics from Complex Analysis
- from Part II - Complex Analysis, Conformal Measures, and Graph Directed Markov Systems
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 249-315
-
- Chapter
- Export citation
9 - Invariant Measures for Holomorphic Maps f in A(X) or in Aw(X)
- from Part II - Complex Analysis, Conformal Measures, and Graph Directed Markov Systems
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 316-341
-
- Chapter
- Export citation
Multiply connected wandering domains of meromorphic functions: the pursuit of uniform internal dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 727-748
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic points of post-critically algebraic holomorphic endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 2382-2414
- Print publication:
- July 2022
-
- Article
- Export citation
Total disconnectedness of Julia sets of random quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1764-1780
- Print publication:
- May 2022
-
- Article
- Export citation
Cubic Polynomials with Periodic Cycles of a Specified Multiplier
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 2 / 16 April 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-344
- Print publication:
- 16 April 2012
-
- Article
-
- You have access
- Export citation
Ergodic properties of semi-hyperbolic functions with polynomial Schwarzian derivative
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 471-502
-
- Article
-
- You have access
- Export citation
Caractérisation des exemples de Lattès et de Kummer
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1235-1270
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation