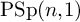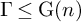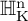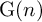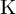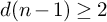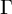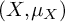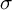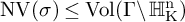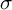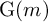Refine search
Actions for selected content:
19 results
Appendix D - Riemann #-functions and meromorphic forms
- from Part III - Appendix
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 391-402
-
- Chapter
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
-
- Article
- Export citation
DECOMPOSITION OF THE JACOBIAN OF SOME TWISTS OF A GENUS
 $2$ CURVE
$2$ CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 445-459
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Multivariate Distributions
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 58-92
-
- Chapter
- Export citation
NATURAL MAPS FOR MEASURABLE COCYCLES OF COMPACT HYPERBOLIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 421-448
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational approximation of a functional of Mumford–Shah typein codimension higher than one
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, pp. 190-221
- Print publication:
- January 2014
-
- Article
- Export citation
An iterative implementation of the implicit nonlinear filter
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 535-543
- Print publication:
- May 2012
-
- Article
- Export citation
Algebraic cycles on the Jacobian of a curve with a linear system of given dimension
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 4 / July 2007
- Published online by Cambridge University Press:
- 17 July 2007, pp. 883-899
- Print publication:
- July 2007
-
- Article
-
- You have access
- Export citation
Algebraic cycles on Jacobian varieties
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 683-688
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation
Torsion Packets on Curves
-
- Journal:
- Compositio Mathematica / Volume 127 / Issue 1 / May 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 109-116
- Print publication:
- May 2001
-
- Article
-
- You have access
- Export citation
Trisecant lines and jacobians, II
-
- Journal:
- Compositio Mathematica / Volume 107 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 177-186
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation