We establish an error term in the Sato–Tate theorem of Birch. That is, for $p$ prime, $q=p^{r}$ and an elliptic curve $E:y^{2}=x^{3}+ax+b$, we show that

$$\begin{eqnarray}\#\{(a,b)\in \mathbb{F}_{q}^{2}:\unicode[STIX]{x1D703}_{a,b}\in I\}=\unicode[STIX]{x1D707}_{ST}(I)q^{2}+O_{r}(q^{7/4})\end{eqnarray}$$

$I\subseteq [0,\unicode[STIX]{x1D70B}]$

$\unicode[STIX]{x1D703}_{a,b}$

$2\sqrt{q}\cos \unicode[STIX]{x1D703}_{a,b}=q+1-E(\mathbb{F}_{q})$

$\unicode[STIX]{x1D707}_{ST}(I)$

$I$

Let $E_{\unicode[STIX]{x1D706}}$ be the Legendre family of elliptic curves. Given $n$ points $P_{1},\ldots ,P_{n}\in E_{\unicode[STIX]{x1D706}}(\overline{\mathbb{Q}(\unicode[STIX]{x1D706})})$, linearly independent over $\mathbb{Z}$, we prove that there are at most finitely many complex numbers $\unicode[STIX]{x1D706}_{0}$ such that $E_{\unicode[STIX]{x1D706}_{0}}$ has complex multiplication and $P_{1}(\unicode[STIX]{x1D706}_{0}),\ldots ,P_{n}(\unicode[STIX]{x1D706}_{0})$ are linearly dependent over End$(E_{\unicode[STIX]{x1D706}_{0}})$. This implies a positive answer to a question of Bertrand and, combined with a previous work in collaboration with Capuano, proves the Zilber–Pink conjecture for a curve in a fibered power of an elliptic scheme when everything is defined over $\overline{\mathbb{Q}}$.

Schmidt [‘Integer points on curves of genus 1’, Compos. Math. 81 (1992), 33–59] conjectured that the number of integer points on the elliptic curve defined by the equation $y^{2}=x^{3}+ax^{2}+bx+c$ , with $a,b,c\in \mathbb{Z}$ , is $O_{\unicode[STIX]{x1D716}}(\max \{1,|a|,|b|,|c|\}^{\unicode[STIX]{x1D716}})$ for any $\unicode[STIX]{x1D716}>0$ . On the other hand, Duke [‘Bounds for arithmetic multiplicities’, Proc. Int. Congress Mathematicians, Vol. II (1998), 163–172] conjectured that the number of algebraic number fields of given degree and discriminant $D$ is $O_{\unicode[STIX]{x1D716}}(|D|^{\unicode[STIX]{x1D716}})$ . In this note, we prove that Duke’s conjecture for quartic number fields implies Schmidt’s conjecture. We also give a short unconditional proof of Schmidt’s conjecture for the elliptic curve $y^{2}=x^{3}+ax$ .

In this paper we study the variation of the $p$ -Selmer rank parities of $p$ -twists of a principally polarized Abelian variety over an arbitrary number field $K$ and show, under certain assumptions, that this parity is periodic with an explicit period. Our result applies in particular to principally polarized Abelian varieties with full $K$ -rational $p$ -torsion subgroup, arbitrary elliptic curves, and Jacobians of hyperelliptic curves. Assuming the Shafarevich–Tate conjecture, our result allows one to classify the rank parities of all quadratic twists of an elliptic or hyperelliptic curve after a finite calculation.

Extending the idea of Dabrowski [‘On the proportion of rank 0 twists of elliptic curves’, C. R. Acad. Sci. Paris, Ser. I 346 (2008), 483–486] and using the 2-descent method, we provide three general families of elliptic curves over $\mathbb{Q}$ such that a positive proportion of prime-twists of such elliptic curves have rank zero simultaneously.

Given an abelian variety 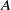$A$ of dimension 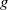$g$ over a number field  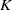$K$ , and a prime 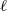$\ell $ , the 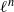${\ell }^{n} $ -torsion points of 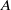$A$ give rise to a representation 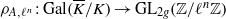${\rho }_{A, {\ell }^{n} } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ( \mathbb{Z} / {\ell }^{n} \mathbb{Z} )$ . In particular, we get a mod- 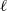$\ell $ representation  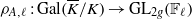${\rho }_{A, \ell } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{F} }_{\ell } )$ and an 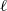$\ell $ -adic representation  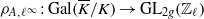${\rho }_{A, {\ell }^{\infty } } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{Z} }_{\ell } )$ . In this paper, we describe the possible determinants of subquotients of these two representations. These two lists turn out to be remarkably similar.

Applying our results in dimension 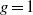$g= 1$ , we recover a generalized version of a theorem of Momose on isogeny characters of elliptic curves over number fields, and obtain, conditionally on the Generalized Riemann Hypothesis, a generalization of Mazur’s bound on rational isogenies of prime degree to number fields.

Let $H$ be a torsion-free compact $p$-adic analytic group whose Lie algebra is split semisimple. We show that the quotient skewfield of fractions of the Iwasawa algebra $\varLambda_H$ of $H$ has trivial centre and use this result to classify the prime $c$-ideals in the Iwasawa algebra $\varLambda_G$ of $G:=H\times\mathbb{Z}_p$. We also show that a finitely generated torsion $\varLambda_G$-module having no non-zero pseudo-null submodule is completely faithful if and only if it is has no central torsion. This has an application to the study of Selmer groups of elliptic curves.

We prove a new formula for the number of integral points on an elliptic curve over a function field without assuming that the coefficient field is algebraically closed. This is an improvement on the standard results of Hindry-Silverman.