We consider an optimal stopping problem of a linear diffusion under Poisson constraint where the agent can adjust the arrival rate of new stopping opportunities. We assume that the agent may switch the rate of the Poisson process between two values. Maintaining the lower rate incurs no cost, whereas the higher rate requires effort that is captured by a cost function c. We study a broad class of payoff functions, cost functions and diffusion dynamics, for which we explicitly characterize the solution to the constrained stopping problem. We also characterize the case where switching to the higher rate is always suboptimal. The results are illustrated with two examples.

We study the behaviour of the norm of the resolvent for non-self-adjoint operators of the form $A := -\partial_x + W(x)$, with $W(x) \ge 0$, defined in ${L^2}({\mathbb{R}})$. We provide a sharp estimate for the norm of its resolvent operator, $\| (A - \lambda)^{-1} \|$, as the spectral parameter diverges $(\lambda \to +\infty)$. Furthermore, we describe the C0-semigroup generated by −A and determine its norm. Finally, we discuss the applications of the results to the asymptotic description of pseudospectra of Schrödinger and damped wave operators, and also the optimality of abstract resolvent bounds based on Carleman-type estimates.

We study an ergodic singular control problem with constraint of a regular one-dimensional linear diffusion. The constraint allows the agent to control the diffusion only at the jump times of an independent Poisson process. Under relatively weak assumptions, we characterize the optimal solution as an impulse-type control policy, where it is optimal to exert the exact amount of control needed to push the process to a unique threshold. Moreover, we discuss the connection of the present problem to ergodic singular control problems, and illustrate the results with different well-known cost and diffusion structures.

We consider the split common null point problem in Hilbert space. We introduce and study a shrinking projection method for finding a solution using the resolvent of a maximal monotone operator and prove a strong convergence theorem for the algorithm.

In this paper, bounded variation control of one-dimensional diffusion processes is considered. We assume that the agent is allowed to control the diffusion only at the jump times of an observable, independent Poisson process. The agent's objective is to maximize the expected present value of the cumulative payoff generated by the controlled diffusion over its lifetime. We propose a relatively weak set of assumptions on the underlying diffusion and the instantaneous payoff structure, under which we solve the problem in closed form. Moreover, we illustrate the main results with an explicit example.

The aim of this paper is to prove the existence and uniqueness of mild and classical solutions of the non-local Cauchy problem for a semilinear integrodifferential equation with deviating argument. The results are established by using the method of semigroups and the contraction mapping principle. The paper generalizes certain results of Lin and Liu.

AMS 2000 Mathematics subject classification: Primary 34K05; 34K30

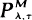The problem of optimal control of a finite dam in the class of policies has been considered by Lam Yeh [6], [7]. In this paper, by using the first Dynkin formula, the same problems of specifying an optimal policy in the class of the policies 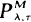to minimize the expected total discounted cost as well as the long-run average cost are considered. Both the expected total discounted cost and long-run average cost are determined explicitly, and then the optimal policy can be found numerically, Also, we obtain the transition density function and the resolvent operator of a reflecting Wiener process.