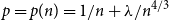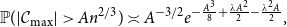Refine search
Actions for selected content:
4 results
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
A note on the Screaming Toes game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 118-130
- Print publication:
- March 2022
-
- Article
- Export citation
The probability of unusually large components in the near-critical Erdős–Rényi graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 245-271
- Print publication:
- March 2018
-
- Article
- Export citation
On the probability of the existence of fixed-size components in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 344-357
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation