We focus on the existence of ground state solutions to the following class of elliptic equations

\begin{equation*}-\Delta_{\mathbb{B}^N} u+V(x)u=f(u) \quad \hbox{in} \quad \mathbb{B}^N,\end{equation*}

where $\mathbb{B}^N$ is the disc model of the Hyperbolic space and $\Delta_{\mathbb{B}^N}$ denotes the Laplace–Beltrami operator with $N \geq 2$, $V:\mathbb{B}^N \to \mathbb{R}$ and $f:\mathbb{R} \to \mathbb{R}$ are continuous functions that satisfy some technical conditions. With different types of the potential V, by introducing some new tricks handling the hurdle that the Hyperbolic space is not a compact manifold, we are able to obtain at least a positive ground state solution using variational methods.

As some applications for the methods adopted above, we derive the existence of normalized solutions to the elliptic problems

\begin{equation*}\left\{\begin{aligned}&-\Delta_{\mathbb{B}^N} u+V(x)u=\mu u+f(u) \quad \hbox{in} \quad \mathbb{B}^N,\\&\int_{\mathbb{B}^N}|u|^{2}\,dV_{{\mathbb{B}^N}}=a^{2},\end{aligned}\right.\end{equation*}

where a > 0, $\mu\in \mathbb{R}$ is an unknown parameter that appears as a Lagrange multiplier and f is a continuous function that fulfils the L2-subcritical or L2-supercritical growth. We do believe that it seems the first results to deal with normalized solutions for the Schrödinger equations in the Hyperbolic space.

In this article, we investigate the following non-linear Schrödinger (NLS) equation with Neumann boundary conditions:

\begin{equation*}\begin{cases}-\Delta u+ \lambda u= f(u) & {\mathrm{in}} \,~ \Omega,\\\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega\end{cases}\end{equation*}

coupled with a constraint condition:

\begin{equation*}\int_{\Omega}|u|^2 dx=c,\end{equation*}

where $\Omega\subset \mathbb{R}^N(N\ge3)$ denotes a smooth bounded domain, ν represents the unit outer normal vector to $\partial \Omega$, c is a positive constant, and λ acts as a Lagrange multiplier. When the non-linearity f exhibits a general mass supercritical growth at infinity, we establish the existence of normalized solutions, which are not necessarily positive solutions and can be characterized as mountain pass type critical points of the associated constraint functional. Our approach provides a uniform treatment of various non-linearities, including cases such as $f(u)=|u|^{p-2}u$, $|u|^{q-2}u+ |u|^{p-2}u$, and $-|u|^{q-2}u+|u|^{p-2}u$, where $2 \lt q \lt 2+\frac{4}{N} \lt p \lt 2^*$. The result is obtained through a combination of a minimax principle with Morse index information for constrained functionals and a novel blow-up analysis for the NLS equation under Neumann boundary conditions.

In this article, we study the following Schrödinger equation

\begin{align*}\begin{cases}-\Delta u -\frac{\mu}{|x|^2} u+\lambda u =f(u), &\text{in}~ \mathbb{R}^N\backslash\{0\},\\\int_{\mathbb{R}^{N}}|u|^{2}\mathrm{d} x=a, & u\in H^1(\mathbb{R}^{N}),\end{cases}\end{align*}

where $N\geq 3$, a > 0, and $\mu \lt \frac{(N-2)^2}{4}$. Here $\frac{1}{|x|^2} $ represents the Hardy potential (or ‘inverse-square potential’), λ is a Lagrange multiplier, and the nonlinearity function f satisfies the general Sobolev critical growth condition. Our main goal is to demonstrate the existence of normalized ground state solutions for this equation when $0 \lt \mu \lt \frac{(N-2)^2}{4}$. We also analyse the behaviour of solutions as $\mu\to0^+$ and derive the existence of normalized ground state solutions for the limiting case where µ = 0. Finally, we investigate the existence of normalized solutions when µ < 0 and analyse the asymptotic behaviour of solutions as $\mu\to 0^-$.

This paper first studies the multiplicity of normalized solutions to the non-autonomous Schrödinger equation with mixed nonlinearities

\begin{equation*}\begin{cases}-\Delta u=\lambda u+h(\epsilon x)|u|^{q-2}u+\eta |u|^{p-2}u,\quad x\in \mathbb{R}^N, \\\int_{\mathbb{R}^N}|u|^2\,\textrm{d}x=a^2,\end{cases}\end{equation*}

$a, \epsilon, \eta \gt 0$

$\lambda\in \mathbb{R}$

$p=2N/(N-2)$

The paper deals with the existence of positive solutions with prescribed $L^2$ norm for the Schrödinger equation

$$-\Delta u+\lambda u+V(x)u=|u|^{p-2}u,\quad u\in H^1_0(\Omega),\quad\int_\Omega u^2{\rm d}\,x=\rho^2,\quad\lambda\in\mathbb{R},$$

$\Omega =\mathbb {R}^N$

$\mathbb {R}^N\setminus \Omega$

$\rho >0$

$V\ge 0$

$V\equiv 0$

$p\in (2,2+\frac 4 N)$

$\bar u$

$V$

$\|V\|_{L^q}$

$q\ge \frac N2$

$q>1$

$N=2$

$V$

$\mathbb {R}^N\setminus \Omega$

$\bar u$

$V\equiv 0$

$\Omega =\mathbb {R}^N$

We consider the mass-critical non-linear Schrödinger equation on non-compact metric graphs. A quite complete description of the structure of the ground states, which correspond to global minimizers of the energy functional under a mass constraint, is provided by Adami, Serra and Tilli in [R. Adami, E. Serra and P. Tilli. Negative energy ground states for the L2-critical NLSE on metric graphs. Comm. Math. Phys. 352 (2017), 387–406.] , where it is proved that existence and properties of ground states depend in a crucial way on both the value of the mass, and the topological properties of the underlying graph. In this paper we address cases when ground states do not exist and show that, under suitable assumptions, constrained local minimizers of the energy do exist. This result paves the way to the existence of stable solutions in the time-dependent equation in cases where the ground state energy level is not achieved.

In this paper, we study the existence, nonexistence and mass concentration of L2-normalized solutions for nonlinear fractional Schrödinger equations. Comparingwith the Schrödinger equation, we encounter some new challenges due to the nonlocal nature of the fractional Laplacian. We first prove that the optimal embedding constant for the fractional Gagliardo–Nirenberg–Sobolev inequality can be expressed by exact form, which improves the results of [17, 18]. By doing this, we then establish the existence and nonexistence of L2-normalized solutions for this equation. Finally, under a certain type of trapping potentials, by using some delicate energy estimates we present a detailed analysis of the concentration behavior of L2-normalized solutions in the mass critical case.

We consider the existence of normalized solutions in H 1(ℝN ) × H 1(ℝN ) for systems of nonlinear Schr¨odinger equations, which appear in models for binary mixtures of ultracold quantum gases. Making a solitary wave ansatz, one is led to coupled systems of elliptic equations of the form

and we are looking for solutions satisfying

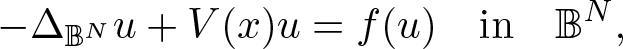
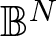
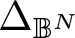
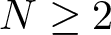
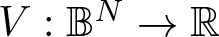
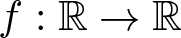
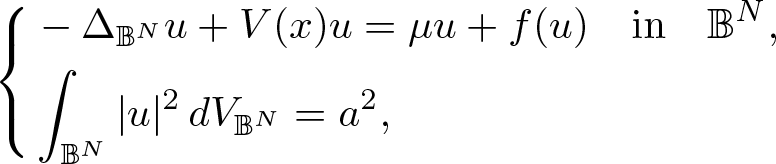
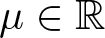
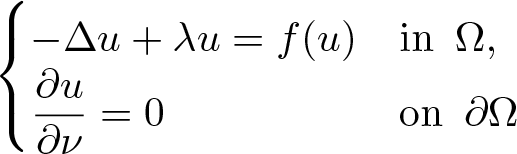
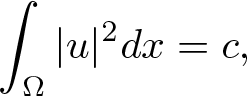
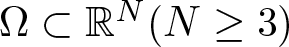
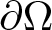
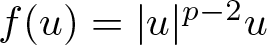
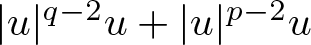
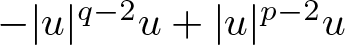
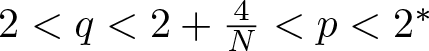
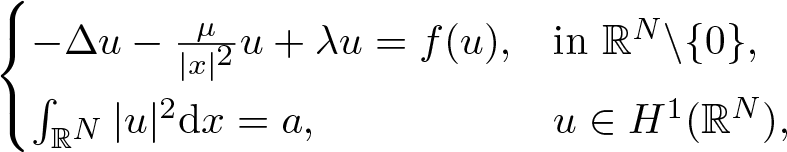
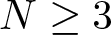
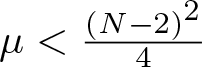
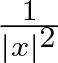
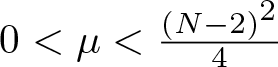
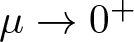
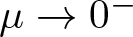
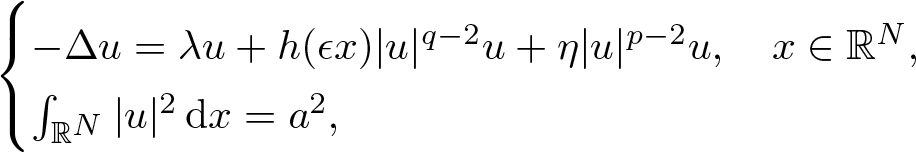
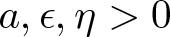
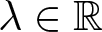
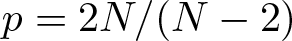
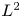
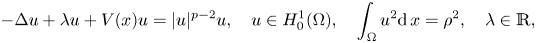
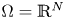
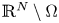
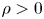
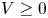
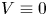
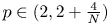
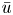
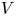
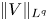
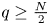
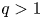
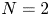
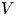
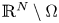
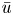
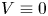
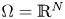
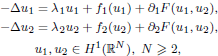
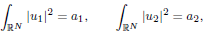
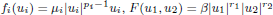where a 1> 0 and a 2> 0 are prescribed. In the system, λ 1 and λ 2 are unknown and will appear as Lagrange multipliers. We treat the case of homogeneous nonlinearities, i.e. , with positive constants 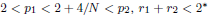β, μi , pi , ri . The exponents are Sobolev subcritical but may be L 2-supercritical. Our main result deals with the case in which in dimensions 2 ≤ N ≤ 4. We also consider the cases in which all of these numbers are less than 2 + 4/N or all are bigger than 2 + 4/N.