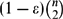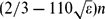Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Path Ramsey Number for Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 612-622
-
- Article
- Export citation

Introduction to Random Graphs
-
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
Perfect Packings in Quasirandom Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 27 October 2015, pp. 595-611
-
- Article
- Export citation
15 - Mappings
- from PART III - Other models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 294-306
-
- Chapter
- Export citation
Contents
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp vii-xii
-
- Chapter
- Export citation
Preface
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp xiii-xviii
-
- Chapter
- Export citation
3 - Vertex Degrees
- from PART I - Basic Models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 48-62
-
- Chapter
- Export citation
4 - Connectivity
- from PART I - Basic Models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 63-70
-
- Chapter
- Export citation
5 - Small Subgraphs
- from PART I - Basic Models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 71-80
-
- Chapter
- Export citation
19 - Brief Notes on Uncovered Topics
- from PART III - Other models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 364-374
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp i-iv
-
- Chapter
- Export citation
11 - Intersection Graphs
- from PART II - Basic Model Extensions
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 202-225
-
- Chapter
- Export citation
Author Index
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 456-461
-
- Chapter
- Export citation
PART IV - Tools and Methods
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 375-376
-
- Chapter
- Export citation
7 - Extreme Characteristics
- from PART I - Basic Models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 110-137
-
- Chapter
- Export citation
14 - Trees
- from PART III - Other models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 263-293
-
- Chapter
- Export citation
17 - Real World Networks
- from PART III - Other models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 329-348
-
- Chapter
- Export citation
22 - Differential Equations Method
- from PART IV - Tools and Methods
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 410-413
-
- Chapter
- Export citation
8 - Extremal Properties
- from PART I - Basic Models
-
- Book:
- Introduction to Random Graphs
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 138-146
-
- Chapter
- Export citation