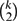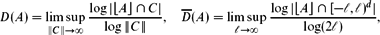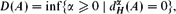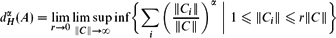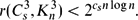Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Saturation in the Hypercube and Bootstrap Percolation
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 31 March 2016, pp. 78-98
-
- Article
- Export citation
Adding Edges to Increase the Chromatic Number of a Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 592-594
-
- Article
- Export citation
A Convexity Property of Discrete Random Walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 928-940
-
- Article
- Export citation
Multivariate Eulerian Polynomials and Exclusion Processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 18 March 2016, pp. 486-499
-
- Article
- Export citation
Marstrand-type Theorems for the Counting and Mass Dimensions in ℤ
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 700-743
-
- Article
- Export citation
Tuza's Conjecture is Asymptotically Tight for Dense Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 645-667
-
- Article
- Export citation
Cycles and Matchings in Randomly Perturbed Digraphs and Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 909-927
-
- Article
- Export citation
Comments on Y. O. Hamidoune's Paper ‘Adding Distinct Congruence Classes’
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 09 March 2016, pp. 641-644
-
- Article
- Export citation
Improved Bounds for the Ramsey Number of Tight Cycles Versus Cliques
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 791-796
-
- Article
- Export citation
On the Normalized Shannon Capacity of a Union
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 766-767
-
- Article
- Export citation
Coexistence in Preferential Attachment Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 09 February 2016, pp. 797-822
-
- Article
- Export citation
10 - Ranking Methods
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 563-616
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp xiii-xviii
-
- Chapter
- Export citation
9 - Rating Systems
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 501-562
-
- Chapter
- Export citation
4 - Smooth Allocation of Prizes
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 157-222
-
- Chapter
- Export citation
7 - Sequential Contests
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 359-442
-
- Chapter
- Export citation
Index
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 713-717
-
- Chapter
- Export citation
2 - Standard All-Pay Contest
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 41-94
-
- Chapter
- Export citation
11 - Appendix
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp 617-680
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Contest Theory
- Published online:
- 05 January 2016
- Print publication:
- 04 February 2016, pp i-iv
-
- Chapter
- Export citation