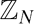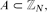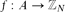Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
CPC volume 22 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation
CPC volume 22 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Freiman Homomorphisms of Random Subsets of
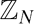 $\mathbb{Z}_{N}$
$\mathbb{Z}_{N}$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 592-611
-
- Article
- Export citation
Lipschitz Functions on Expanders are Typically Flat
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 566-591
-
- Article
- Export citation
Reimer's Inequality on a Finite Distributive Lattice
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 612-621
-
- Article
- Export citation

Boolean Models and Methods in Mathematics, Computer Science, and Engineering
-
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010

Solving Polynomial Equation Systems II
- Macaulay's Paradigm and Gröbner Technology
-
- Published online:
- 05 June 2013
- Print publication:
- 05 May 2005
Acknowledgements
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp xiii-xiv
-
- Chapter
- Export citation
1 - Permutations
- from PART ONE - THEORY
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 13-28
-
- Chapter
- Export citation
0 - Introduction
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 1-10
-
- Chapter
- Export citation
6 - Equivalents of Nom
- from PART ONE - THEORY
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 95-110
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp i-iv
-
- Chapter
- Export citation
8 - Nominal algebraic data types
- from PART TWO - APPLICATIONS
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 129-152
-
- Chapter
- Export citation
PART ONE - THEORY
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 11-12
-
- Chapter
- Export citation
9 - Locally scoped names
- from PART TWO - APPLICATIONS
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 153-176
-
- Chapter
- Export citation
2 - Support
- from PART ONE - THEORY
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 29-48
-
- Chapter
- Export citation
Contents
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp vii-x
-
- Chapter
- Export citation
PART TWO - APPLICATIONS
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 111-112
-
- Chapter
- Export citation
References
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 257-268
-
- Chapter
- Export citation
12 - Computational logic
- from PART TWO - APPLICATIONS
-
- Book:
- Nominal Sets
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013, pp 240-256
-
- Chapter
- Export citation