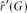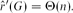Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry

Surveys in Combinatorics 2013
-
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013

Nominal Sets
- Names and Symmetry in Computer Science
-
- Published online:
- 05 July 2013
- Print publication:
- 30 May 2013
Non-Deterministic Graph Property Testing
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 5 / September 2013
- Published online by Cambridge University Press:
- 03 July 2013, pp. 749-762
-
- Article
-
- You have access
- Export citation
Analysis of a near-metric TSP approximation algorithm∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 06 August 2013, pp. 293-314
- Print publication:
- July 2013
-
- Article
- Export citation
Minimal 2-dominating sets in trees∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 08 July 2013, pp. 235-240
- Print publication:
- July 2013
-
- Article
- Export citation
Factoring and testing primes in small space∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 241-259
- Print publication:
- July 2013
-
- Article
- Export citation
New applications of the wreath product of forest algebras∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 261-291
- Print publication:
- July 2013
-
- Article
- Export citation
9 - Automatic counting of tilings of skinny plane regions
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 363-378
-
- Chapter
- Export citation
4 - The complexity of change
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 127-160
-
- Chapter
- Export citation
Contents
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp v-vi
-
- Chapter
- Export citation
7 - The world of hereditary graph classes viewed through Truemper configurations
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 265-326
-
- Chapter
- Export citation
3 - Bent functions and their connections to combinatorics
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 91-126
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp i-iv
-
- Chapter
- Export citation
5 - How symmetric can maps on surfaces be?
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 161-238
-
- Chapter
- Export citation
2 - The geometry of covering codes: small complete caps and saturating sets in Galois spaces
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 51-90
-
- Chapter
- Export citation
Preface
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp vii-viii
-
- Chapter
- Export citation
6 - Some open problems on permutation patterns
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 239-264
-
- Chapter
- Export citation
8 - Structure in minor-closed classes of matroids
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 327-362
-
- Chapter
- Export citation
1 - Graph removal lemmas
-
-
- Book:
- Surveys in Combinatorics 2013
- Published online:
- 05 July 2013
- Print publication:
- 27 June 2013, pp 1-50
-
- Chapter
- Export citation
Size Ramsey Number of Bounded Degree Graphs for Games
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 499-516
-
- Article
- Export citation