Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
CPC volume 20 issue 5 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Concave Majorants of Random Walks and Related Poisson Processes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 651-682
-
- Article
- Export citation
On the Distribution of Three-Term Arithmetic Progressions in Sparse Subsets of Fpn
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 777-791
-
- Article
- Export citation
CPC volume 20 issue 5 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
YAHYA OULD HAMIDOUNE the Mauritanian mathematician 1948 – 11 March 2011
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 641-645
-
- Article
-
- You have access
- Export citation
Daisies and Other Turán Problems
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 743-747
-
- Article
- Export citation
PHILIPPE FLAJOLET 1 December 1948 – 22 March 2011
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 647-649
-
- Article
-
- You have access
- Export citation
On r-Cross Intersecting Families of Sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 749-752
-
- Article
- Export citation
On Sumsets of Convex Sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 07 July 2011, pp. 793-798
-
- Article
- Export citation
A note on maximum independent sets and minimum clique partitions in unit disk graphs and penny graphs: complexity and approximation
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 05 September 2011, pp. 331-346
- Print publication:
- July 2011
-
- Article
- Export citation
The Fibonacci automorphismof free Burnside groups
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 26 August 2011, pp. 301-309
- Print publication:
- July 2011
-
- Article
- Export citation
Construction of tree automata from regular expressions
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 22 August 2011, pp. 347-370
- Print publication:
- July 2011
-
- Article
- Export citation
Locally catenative sequencesand Turtle graphics
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 22 August 2011, pp. 311-330
- Print publication:
- July 2011
-
- Article
- Export citation
Deciding knowledge in security protocols under some e-voting theories
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 26 August 2011, pp. 269-299
- Print publication:
- July 2011
-
- Article
- Export citation
Zero Biasing and Jack Measures
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 753-762
-
- Article
- Export citation
An Improvement of the Lovász Local Lemma via Cluster Expansion
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 709-719
-
- Article
- Export citation
Karp–Sipser on Random Graphs with a Fixed Degree Sequence
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 721-741
-
- Article
- Export citation
First Passage Percolation on the Erdős–Rényi Random Graph
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 683-707
-
- Article
- Export citation
Random Graphs with Few Disjoint Cycles
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 763-775
-
- Article
- Export citation

Lectures in Game Theory for Computer Scientists
-
- Published online:
- 01 June 2011
- Print publication:
- 06 January 2011
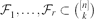 . Suppose that
. Suppose that 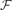
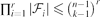 .
.