Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
CPC volume 20 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
CPC volume 20 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation
The Maximum Degree of Series-Parallel Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 529-570
-
- Article
- Export citation
Better Bounds for k-Partitions of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 631-640
-
- Article
- Export citation
3 - Rounding Data and Dynamic Programming
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 57-72
-
- Chapter
- Export citation
I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 1-2
-
- Chapter
- Export citation
4 - Deterministic Rounding of Linear Programs
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 73-98
-
- Chapter
- Export citation
15 - Further Uses of Cuts and Metrics
- from II - Further Uses of the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 369-408
-
- Chapter
- Export citation
1 - An Introduction to Approximation Algorithms
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 3-26
-
- Chapter
- Export citation
17 - Open Problems
- from II - Further Uses of the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 453-458
-
- Chapter
- Export citation
14 - Further Uses of the Primal-Dual Method
- from II - Further Uses of the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 355-368
-
- Chapter
- Export citation
6 - Randomized Rounding of Semidefinite Programs
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 137-156
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp i-iv
-
- Chapter
- Export citation
Preface
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp ix-xii
-
- Chapter
- Export citation
II - Further Uses of the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 229-230
-
- Chapter
- Export citation
7 - The Primal-Dual Method
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 157-192
-
- Chapter
- Export citation
Bibliography
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 469-484
-
- Chapter
- Export citation
Appendix A - Linear Programming
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 459-464
-
- Chapter
- Export citation
2 - Greedy Algorithms and Local Search
- from I - An Introduction to the Techniques
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp 27-56
-
- Chapter
- Export citation
Contents
-
- Book:
- The Design of Approximation Algorithms
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2011, pp v-viii
-
- Chapter
- Export citation

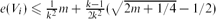 for
for 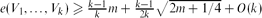 , where
, where 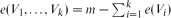 . This answers a problem of Bollobás and Scott [2] in the affirmative. Moreover,
. This answers a problem of Bollobás and Scott [2] in the affirmative. Moreover, 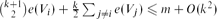 for
for 