Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
On Barycentric Subdivision
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 24 November 2010, pp. 213-237
-
- Article
- Export citation

Permutation Patterns
-
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010
Diameters in Supercritical Random Graphs Via First Passage Percolation
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. 729-751
-
- Article
- Export citation
CPC volume 19 issue 5-6 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Introduction
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, p. 641
-
- Article
- Export citation
The Diameter of Sparse Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. 835-926
-
- Article
- Export citation
On Random Betweenness Constraints
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. 775-790
-
- Article
- Export citation
CPC volume 19 issue 5-6 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Sturmian jungle (or garden?)on multiliteral alphabets
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 443-470
- Print publication:
- October 2010
-
- Article
- Export citation
Classes of two-dimensional languagesand recognizability conditions
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 471-488
- Print publication:
- October 2010
-
- Article
- Export citation
Quantum coherent spaces and linear logic
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 October 2010, pp. 419-441
- Print publication:
- October 2010
-
- Article
- Export citation
Translation from classical two-way automata to pebble two-way automata
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 507-523
- Print publication:
- October 2010
-
- Article
- Export citation
The code problem for directed figures
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 489-506
- Print publication:
- October 2010
-
- Article
- Export citation
A CAT algorithm for the exhaustive generation of ice piles
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 525-543
- Print publication:
- October 2010
-
- Article
- Export citation
Graphs, Links, and Duality on Surfaces
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 29 September 2010, pp. 267-287
-
- Article
- Export citation
Period Lengths for Iterated Functions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 16 September 2010, pp. 289-298
-
- Article
- Export citation
15 - Arbitrarily high order of convergence of the worst-case error
-
- Book:
- Digital Nets and Sequences
- Published online:
- 05 July 2014
- Print publication:
- 09 September 2010, pp 465-508
-
- Chapter
- Export citation
14 - The decay of the Walsh coefficients of smooth functions
-
- Book:
- Digital Nets and Sequences
- Published online:
- 05 July 2014
- Print publication:
- 09 September 2010, pp 434-464
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Digital Nets and Sequences
- Published online:
- 05 July 2014
- Print publication:
- 09 September 2010, pp i-iv
-
- Chapter
- Export citation
Dedication
-
- Book:
- Digital Nets and Sequences
- Published online:
- 05 July 2014
- Print publication:
- 09 September 2010, pp v-vi
-
- Chapter
- Export citation
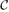
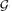
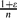 where ε
where ε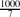 .
.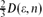 , and the maximal distance in
, and the maximal distance in 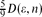 .
.