Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Enumerated type semantics for the calculus of looping sequences
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 35-58
- Print publication:
- January 2011
-
- Article
- Export citation
Idealized coinductive type systemsfor imperative object-oriented programs
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 3-33
- Print publication:
- January 2011
-
- Article
- Export citation
Extending the lambda-calculuswith unbind and rebind
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 143-162
- Print publication:
- January 2011
-
- Article
- Export citation
Local Resilience and Hamiltonicity Maker–Breaker Games in Random Regular Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 16 December 2010, pp. 173-211
-
- Article
- Export citation
A Lower Bound for the Size of a Minkowski Sum of Dilates
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 249-256
-
- Article
- Export citation
CPC volume 20 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 03 December 2010, pp. b1-b2
-
- Article
-
- You have access
- Export citation
CPC volume 20 issue 1 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 03 December 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The Dual BKR Inequality and Rudich's Conjecture
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 02 December 2010, pp. 257-266
-
- Article
- Export citation
References
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 191-206
-
- Chapter
- Export citation
3 - Floating-point arithmetic
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 79-124
-
- Chapter
- Export citation
5 - Implementations and pointers
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 185-190
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp i-iv
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp xi-xii
-
- Chapter
- Export citation
Preface
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp ix-x
-
- Chapter
- Export citation
Index
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 207-221
-
- Chapter
- Export citation
Contents
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp v-viii
-
- Chapter
- Export citation
1 - Integer arithmetic
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 1-46
-
- Chapter
- Export citation
2 - Modular arithmetic and the FFT
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 47-78
-
- Chapter
- Export citation
4 - Elementary and special function evaluation
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp 125-184
-
- Chapter
- Export citation
Notation
-
- Book:
- Modern Computer Arithmetic
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010, pp xiii-xvi
-
- Chapter
- Export citation
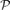
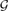
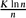 then, with high probability, the local resilience of
then, with high probability, the local resilience of 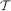
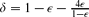 . (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)
. (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)