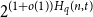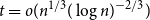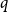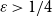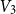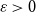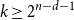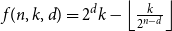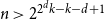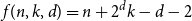Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Chapter 11 - Heap
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 487-502
-
- Chapter
- Export citation
Contents
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp vii-xx
-
- Chapter
- Export citation
Chapter 14 - Hashing
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 605-628
-
- Chapter
- Export citation
Chapter 2 - Introduction to Algorithm
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 15-40
-
- Chapter
- Export citation
Chapter 10 - Trees
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 391-486
-
- Chapter
- Export citation
Chapter 7 - Linked List
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 207-310
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp xxiii-xxiv
-
- Chapter
- Export citation
Chapter 13 - Searching and Sorting
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 557-604
-
- Chapter
- Export citation
Chapter 3 - Array
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 41-84
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp i-iv
-
- Chapter
- Export citation
Chapter 12 - Graphs
-
- Book:
- Data Structures and Algorithms Using Python
- Published online:
- 30 April 2025
- Print publication:
- 15 June 2023, pp 503-556
-
- Chapter
- Export citation
Archaeology of random recursive dags and Cooper-Frieze random networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 13 June 2023, pp. 859-873
-
- Article
- Export citation
On the number of error correcting codes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 819-832
-
- Article
- Export citation
Spanning
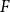 $F$-cycles in random graphs
$F$-cycles in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 833-850
-
- Article
- Export citation
Unimodular random one-ended planar graphs are sofic
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 851-858
-
- Article
- Export citation

Introduction to Proofs and Proof Strategies
-
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023
-
- Textbook
- Export citation

Pearls of Algorithm Engineering
-
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023
A smoother notion of spread hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 809-818
-
- Article
- Export citation
Unavoidable patterns in locally balanced colourings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 01 June 2023, pp. 796-808
-
- Article
- Export citation
Subspace coverings with multiplicities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 782-795
-
- Article
-
- You have access
- Open access
- HTML
- Export citation