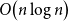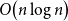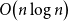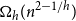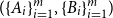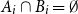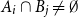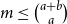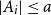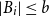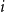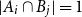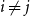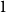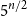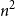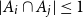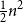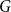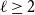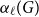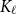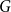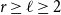Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
A pair degree condition for Hamiltonian cycles in 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 762-781
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal geometric graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Online and Matching-Based Market Design
-
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023
Maximal chordal subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 724-741
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey upper density of infinite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clique-factors in graphs with sublinear
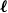 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 665-681
-
- Article
- Export citation
Expected number of faces in a random embedding of any graph is at most linear
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 682-690
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 251-256
-
- Chapter
- Export citation
List of Notation
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp ix-x
-
- Chapter
- Export citation
8 - Theory of Computation
- from Part II - Solutions
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 193-249
-
- Chapter
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Part II - Solutions
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 53-54
-
- Chapter
- Export citation
Part I - Problems
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 1-2
-
- Chapter
- Export citation
3 - Context-Free Languages
- from Part I - Problems
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 26-40
-
- Chapter
- Export citation
Contents
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp v-vi
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp i-iv
-
- Chapter
- Export citation
4 - Theory of Computation
- from Part I - Problems
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 41-52
-
- Chapter
- Export citation
Further Reading
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 250-250
-
- Chapter
- Export citation
7 - Context-Free Languages
- from Part II - Solutions
-
- Book:
- 200 Problems on Languages, Automata, and Computation
- Published online:
- 14 April 2023
- Print publication:
- 20 April 2023, pp 129-192
-
- Chapter
- Export citation