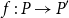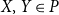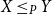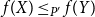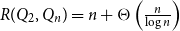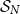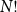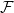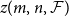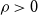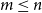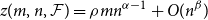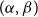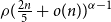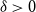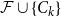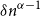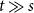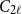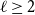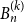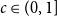Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
References
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 210-215
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp i-iv
-
- Chapter
- Export citation
14 - Weighted Graphs
- from Part III - Modeling Complex Networks
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 197-209
-
- Chapter
- Export citation
1 - Introduction
- from Part I - Preliminaries
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 3-7
-
- Chapter
- Export citation
Contents
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp vii-viii
-
- Chapter
- Export citation
6 - Connectivity
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 78-84
-
- Chapter
- Export citation
8 - Large Subgraphs
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 93-110
-
- Chapter
- Export citation
Part I - Preliminaries
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 1-2
-
- Chapter
- Export citation
4 - Evolution
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 45-63
-
- Chapter
- Export citation
11 - Small World
- from Part III - Modeling Complex Networks
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 154-162
-
- Chapter
- Export citation
9 - Extreme Characteristics
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 111-124
-
- Chapter
- Export citation
Preface
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp ix-ix
-
- Chapter
- Export citation

Random Graphs and Networks: A First Course
-
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023
Poset Ramsey numbers: large Boolean lattice versus a fixed poset
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 638-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random feedback shift registers and the limit distribution for largest cycle lengths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 559-593
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bipartite-ness under smooth conditions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 546-558
-
- Article
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
Off-diagonal book Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 516-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Connecting Discrete Mathematics and Computer Science
-
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022
-
- Textbook
- Export citation