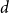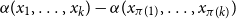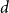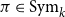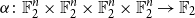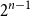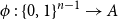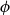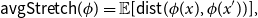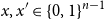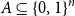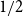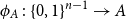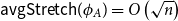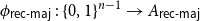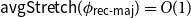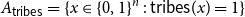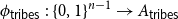Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Copyright page
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp iv-iv
-
- Chapter
- Export citation
Dedication
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp v-vi
-
- Chapter
- Export citation
Nomenclature
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp xiii-xvi
-
- Chapter
- Export citation
7 - Synchronisation
- from II - Mathematical Tools of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 163-176
-
- Chapter
- Export citation
3 - Specific Types of Emergent Behaviour
- from I - Conceptual Foundation of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 46-74
-
- Chapter
- Export citation
Contents
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp vii-x
-
- Chapter
- Export citation
Index
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 436-440
-
- Chapter
- Export citation
I - Conceptual Foundation of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 1-86
-
- Chapter
- Export citation
Glossary
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 401-410
-
- Chapter
- Export citation
2 - Conceptual Framework of Emergence
- from I - Conceptual Foundation of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 21-45
-
- Chapter
- Export citation
12 - Intermittency
- from II - Mathematical Tools of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 356-386
-
- Chapter
- Export citation
1 - The Science of Emergence
- from I - Conceptual Foundation of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 5-20
-
- Chapter
- Export citation
Preface
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp xvii-xx
-
- Chapter
- Export citation
References
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 411-435
-
- Chapter
- Export citation
5 - Branching Processes
- from II - Mathematical Tools of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 93-109
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp xi-xii
-
- Chapter
- Export citation
8 - Network Theory
- from II - Mathematical Tools of Complexity Science
-
- Book:
- Complexity Science
- Published online:
- 13 December 2022
- Print publication:
- 17 November 2022, pp 177-229
-
- Chapter
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximately symmetric forms far from being exactly symmetric
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 299-315
-
- Article
- Export citation
On mappings on the hypercube with small average stretch
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 334-348
-
- Article
- Export citation