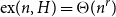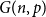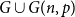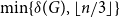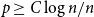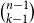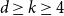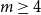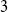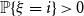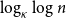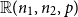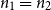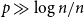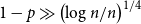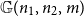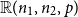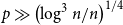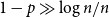Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
6 - Analysis of Algorithms
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 267-326
-
- Chapter
- Export citation
References
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 661-666
-
- Chapter
- Export citation
3 - Logic
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 79-142
-
- Chapter
- Export citation
12 - Looking Forward
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 657-660
-
- Chapter
- Export citation
11 - Graphs and Trees
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 577-656
-
- Chapter
- Export citation
Index
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 667-676
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp xiii-xiv
-
- Chapter
- Export citation
Credits
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp xv-xvi
-
- Chapter
- Export citation
5 - Mathematical Induction
-
- Book:
- Connecting Discrete Mathematics and Computer Science
- Published online:
- 16 December 2022
- Print publication:
- 04 August 2022, pp 215-266
-
- Chapter
- Export citation
A BK inequality for random matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Many Turán exponents via subdivisions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 July 2022, pp. 134-150
-
- Article
- Export citation
Clustered colouring of graph classes with bounded treedepth or pathwidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 122-133
-
- Article
- Export citation
Triangles in randomly perturbed graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 91-121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Percolation in Spatial Networks
- Spatial Network Models Beyond Nearest Neighbours Structures
-
- Published online:
- 15 June 2022
- Print publication:
- 14 July 2022
-
- Element
- Export citation
Complete subgraphs in a multipartite graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1092-1101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypergraphs without non-trivial intersecting subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1076-1091
-
- Article
- Export citation
On the peel number and the leaf-height of Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 68-90
-
- Article
- Export citation
Colouring graphs with forbidden bipartite subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 June 2022, pp. 45-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sandwiching biregular random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Community detection and percolation of information in a geometric setting
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2022, pp. 1048-1069
-
- Article
-
- You have access
- Open access
- HTML
- Export citation