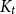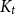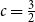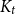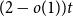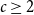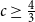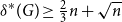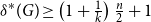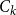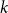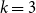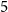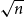Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Improved lower bound for the list chromatic number of graphs with no Kt minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1070-1075
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1031-1047
-
- Article
- Export citation
On tripartite common graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 May 2022, pp. 907-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The diameter of the uniform spanning tree of dense graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1010-1030
-
- Article
- Export citation
3 - Operator Calculus: The Mapping between Vector Spaces
- from Part I - Operator Graph Theory
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 88-116
-
- Chapter
- Export citation
4 - Graphs with Imprimitive Automorphism Group
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 132-166
-
- Chapter
- Export citation
6 - Other Classes of Graphs
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 214-271
-
- Chapter
- Export citation
7 - The Cayley Isomorphism Problem
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 272-321
-
- Chapter
- Export citation
Index of Symbols
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 500-502
-
- Chapter
- Export citation
2 - Classical Graph Theory: The Mathematical Description of Networks
- from Part I - Operator Graph Theory
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 13-87
-
- Chapter
- Export citation
Preface
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp ix-xii
-
- Chapter
- Export citation
Bibliography
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 327-332
-
- Chapter
- Export citation
Subject Index
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 336-342
-
- Chapter
- Export citation
13 - Graphs with Other Types of Symmetry: Half-arc-transitive Graphs and Semisymmetric Graphs
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 451-467
-
- Chapter
- Export citation
References
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 474-496
-
- Chapter
- Export citation
4 - Operator Graph Theory: The Mathematics of Finite Networks
- from Part I - Operator Graph Theory
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 117-178
-
- Chapter
- Export citation
Afterthought
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 325-326
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 1-10
-
- Chapter
- Export citation
Index of Graphs
-
- Book:
- Symmetry in Graphs
- Published online:
- 28 April 2022
- Print publication:
- 12 May 2022, pp 497-499
-
- Chapter
- Export citation
6 - Measuring Graphs
- from Part II - Applications
-
- Book:
- The Mathematics of Finite Networks
- Published online:
- 30 April 2022
- Print publication:
- 12 May 2022, pp 238-290
-
- Chapter
- Export citation