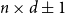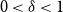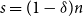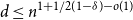Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Polynomials over structured grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
Sparse recovery properties of discrete random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 316-325
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved bound for improper colourings of graphs with no odd clique minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 326-333
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Words and sequences
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 10-31
-
- Chapter
- Export citation
8 - First-order formulas for fundamental sequence properties
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 113-192
-
- Chapter
- Export citation
6 - First-order logic and automatic sequences
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 82-95
-
- Chapter
- Export citation
7 - Using Walnut
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 96-112
-
- Chapter
- Export citation
Permissions
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp xiv-xvi
-
- Chapter
- Export citation
10 - Synchronized sequences
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 237-302
-
- Chapter
- Export citation
Bibliography
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 330-349
-
- Chapter
- Export citation
Contents
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp vii-x
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 1-9
-
- Chapter
- Export citation
Index
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 350-358
-
- Chapter
- Export citation
11 - Additive number theory
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 303-315
-
- Chapter
- Export citation
13 - A final word
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 327-329
-
- Chapter
- Export citation
Preface
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp xi-xiii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp i-vi
-
- Chapter
- Export citation
5 - Automatic sequences
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 62-81
-
- Chapter
- Export citation
4 - Automata
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 47-61
-
- Chapter
- Export citation
3 - Number representations and numeration systems
-
- Book:
- The Logical Approach to Automatic Sequences
- Published online:
- 09 September 2022
- Print publication:
- 29 September 2022, pp 32-46
-
- Chapter
- Export citation