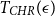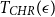Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
6 - Van Der Waerden’s Theorem
-
- Book:
- The Discrete Mathematical Charms of Paul Erdos
- Published online:
- 05 August 2021
- Print publication:
- 26 August 2021, pp 82-96
-
- Chapter
- Export citation
Appendix C - More on Erdős
-
- Book:
- The Discrete Mathematical Charms of Paul Erdos
- Published online:
- 05 August 2021
- Print publication:
- 26 August 2021, pp 218-225
-
- Chapter
- Export citation
Introduction
-
- Book:
- The Discrete Mathematical Charms of Paul Erdos
- Published online:
- 05 August 2021
- Print publication:
- 26 August 2021, pp 1-2
-
- Chapter
- Export citation
On the mixing time of coordinate Hit-and-Run
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 320-332
-
- Article
- Export citation
10 - Game Trees with Imperfect Information
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 263-298
-
- Chapter
- Export citation
2 - Congestion Games
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 39-52
-
- Chapter
- Export citation
3 - Games in Strategic Form
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 53-76
-
- Chapter
- Export citation
12 - Correlated Equilibrium
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 333-350
-
- Chapter
- Export citation
References
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 351-357
-
- Chapter
- Export citation
Index
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 358-362
-
- Chapter
- Export citation
8 - Zero-Sum Games
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 205-222
-
- Chapter
- Export citation
5 - Expected Utility
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 103-134
-
- Chapter
- Export citation
7 - Brouwer’s Fixed-Point Theorem
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 169-204
-
- Chapter
- Export citation
Preface
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp ix-xii
-
- Chapter
- Export citation
9 - Geometry of Equilibria in Bimatrix Games
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 223-262
-
- Chapter
- Export citation
4 - Game Trees with Perfect Information
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 77-102
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp iv-iv
-
- Chapter
- Export citation
Reviews
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp ii-ii
-
- Chapter
- Export citation
1 - Nim and Combinatorial Games
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp 1-38
-
- Chapter
- Export citation
Contents
-
- Book:
- Game Theory Basics
- Published online:
- 22 October 2021
- Print publication:
- 19 August 2021, pp v-viii
-
- Chapter
- Export citation