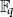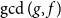Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Dedication
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp v-vi
-
- Chapter
- Export citation
Bibliography
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 602-608
-
- Chapter
- Export citation
Short Answers for Selected Problems
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 531-532
-
- Chapter
- Export citation
10 - Graph Theory
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 361-452
-
- Chapter
- Export citation
Short Answers for Warm-Up Problems
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 522-523
-
- Chapter
- Export citation
Contents
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp vii-x
-
- Chapter
- Export citation
1 - Induction and Recurrence Relations
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 6-41
-
- Chapter
- Export citation
8 - The Inclusion–Exclusion Principle
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 261-291
-
- Chapter
- Export citation
11 - Posets, Matchings, and Boolean Lattices
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 453-521
-
- Chapter
- Export citation
7 - Integer Partitions
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 230-260
-
- Chapter
- Export citation
5 - Binomial and Multinomial Coefficients
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 147-192
-
- Chapter
- Export citation
9 - Generating Functions
-
- Book:
- An Invitation to Combinatorics
- Published online:
- 16 September 2021
- Print publication:
- 22 July 2021, pp 292-360
-
- Chapter
- Export citation
Perfect matchings, rank of connection tensors and graph homomorphisms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 19 July 2021, pp. 268-303
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
On directed analogues of expander and hyperfinite graph sequences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 184-197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
5 - Regularities inWords
-
- Book:
- 125 Problems in Text Algorithms
- Published online:
- 10 June 2021
- Print publication:
- 01 July 2021, pp 180-229
-
- Chapter
- Export citation
7 - Miscellaneous
-
- Book:
- 125 Problems in Text Algorithms
- Published online:
- 10 June 2021
- Print publication:
- 01 July 2021, pp 275-317
-
- Chapter
- Export citation
3 - Pattern Matching
-
- Book:
- 125 Problems in Text Algorithms
- Published online:
- 10 June 2021
- Print publication:
- 01 July 2021, pp 53-110
-
- Chapter
- Export citation
4 - Efficient Data Structures
-
- Book:
- 125 Problems in Text Algorithms
- Published online:
- 10 June 2021
- Print publication:
- 01 July 2021, pp 111-179
-
- Chapter
- Export citation