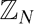Refine search
Actions for selected content:
48287 results in Computer Science
4 - Definability, unification and matching
- from Part I - Simple Types λA→
-
-
- Book:
- Lambda Calculus with Types
- Published online:
- 05 August 2013
- Print publication:
- 20 June 2013, pp 192-242
-
- Chapter
- Export citation
Indices
-
- Book:
- Lambda Calculus with Types
- Published online:
- 05 August 2013
- Print publication:
- 20 June 2013, pp 814-814
-
- Chapter
- Export citation
STRONG COMPLETENESS OF S4 FOR ANY DENSE-IN-ITSELF METRIC SPACE
-
- Journal:
- The Review of Symbolic Logic / Volume 6 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 545-570
- Print publication:
- September 2013
-
- Article
- Export citation
6 - Applications
- from Part I - Simple Types λA→
-
-
- Book:
- Lambda Calculus with Types
- Published online:
- 05 August 2013
- Print publication:
- 20 June 2013, pp 323-376
-
- Chapter
- Export citation
Index of terms
- from Indices
-
- Book:
- Lambda Calculus with Types
- Published online:
- 05 August 2013
- Print publication:
- 20 June 2013, pp 815-822
-
- Chapter
- Export citation
Index of Citations
- from Indices
-
- Book:
- Lambda Calculus with Types
- Published online:
- 05 August 2013
- Print publication:
- 20 June 2013, pp 823-827
-
- Chapter
- Export citation
Improving shift-reduce constituency parsing with large-scale unlabeled data
-
- Journal:
- Natural Language Engineering / Volume 21 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 June 2013, pp. 113-138
-
- Article
- Export citation
Trace spaces of directed tori with rectangular holes
-
- Journal:
- Mathematical Structures in Computer Science / Volume 24 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 17 June 2013, e240202
-
- Article
- Export citation
Size Ramsey Number of Bounded Degree Graphs for Games
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 499-516
-
- Article
- Export citation
CPC volume 22 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation
CPC volume 22 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Freiman Homomorphisms of Random Subsets of
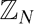 $\mathbb{Z}_{N}$
$\mathbb{Z}_{N}$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 592-611
-
- Article
- Export citation
Lipschitz Functions on Expanders are Typically Flat
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 4 / July 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 566-591
-
- Article
- Export citation