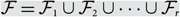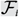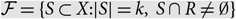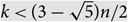Refine search
Actions for selected content:
48196 results in Computer Science
1 - Introduction
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 1-8
-
- Chapter
- Export citation
Contents
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp ix-xi
-
- Chapter
- Export citation
Dedication
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp vii-viii
-
- Chapter
- Export citation
Endorsements
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp i-ii
-
- Chapter
- Export citation
A natural barrier in random greedy hypergraph matching
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 27 June 2019, pp. 816-825
-
- Article
- Export citation
7 - Equilibrium Programming with Equilibrium Constraints
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 144-167
-
- Chapter
- Export citation
9 - Applications of Game Theory in the Internet of Things
- from Part II - Applications
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 195-257
-
- Chapter
- Export citation
8 - Miscellaneous Games
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 168-192
-
- Chapter
- Export citation
14 - 4G, 5G, and Beyond
- from Part II - Applications
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 377-424
-
- Chapter
- Export citation
5 - Games with Bounded Rationality
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 112-122
-
- Chapter
- Export citation
4 - Stochastic Games
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 108-111
-
- Chapter
- Export citation
Index
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 494-496
-
- Chapter
- Export citation
2 - Matching Games
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 11-37
-
- Chapter
- Export citation
Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 9-10
-
- Chapter
- Export citation
Part II - Applications
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 193-194
-
- Chapter
- Export citation
15 - Security
- from Part II - Applications
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 425-458
-
- Chapter
- Export citation
On the union of intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 27 June 2019, pp. 826-839
-
- Article
- Export citation
10 - Applications of Game Theory in Network Virtualization
- from Part II - Applications
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 258-269
-
- Chapter
- Export citation
3 - Contract Theory
- from Part I - Theory
-
- Book:
- Game Theory for Next Generation Wireless and Communication Networks
- Published online:
- 13 June 2019
- Print publication:
- 27 June 2019, pp 38-107
-
- Chapter
- Export citation