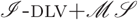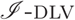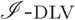Refine search
Actions for selected content:
48196 results in Computer Science
Contents
-
- Book:
- Abstract Recursion and Intrinsic Complexity
- Published online:
- 23 November 2018
- Print publication:
- 06 December 2018, pp v-viii
-
- Chapter
- Export citation
3 - Complexity theory for recursive programs
- from Part I - Abstract (first order) recursion
-
- Book:
- Abstract Recursion and Intrinsic Complexity
- Published online:
- 23 November 2018
- Print publication:
- 06 December 2018, pp 103-126
-
- Chapter
- Export citation
Introduction
-
- Book:
- Abstract Recursion and Intrinsic Complexity
- Published online:
- 23 November 2018
- Print publication:
- 06 December 2018, pp 1-6
-
- Chapter
- Export citation
CARNAP’S DEFENSE OF IMPREDICATIVE DEFINITIONS
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 372-404
- Print publication:
- June 2019
-
- Article
- Export citation
A NOTE ON RÉNYI'S ENTROPY RATE FOR TIME-INHOMOGENEOUS MARKOV CHAINS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 579-590
-
- Article
- Export citation
ON DETERMINISTIC FINITE STATE MACHINES IN RANDOM ENVIRONMENTS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 528-563
-
- Article
- Export citation
FREGE’S CONSTRAINT AND THE NATURE OF FREGE’S FOUNDATIONAL PROGRAM
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 97-143
- Print publication:
- March 2019
-
- Article
- Export citation
APPROXIMATION OF THE TAIL PROBABILITIES FOR BIDIMENSIONAL RANDOMLY WEIGHTED SUMS WITH DEPENDENT COMPONENTS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 December 2018, pp. 112-130
-
- Article
- Export citation
WINNER PLAYS STRUCTURE IN RANDOM KNOCKOUT TOURNAMENTS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 500-510
-
- Article
- Export citation
Reward shaping for knowledge-based multi-objective multi-agent reinforcement learning
- Part of
-
- Journal:
- The Knowledge Engineering Review / Volume 33 / 2018
- Published online by Cambridge University Press:
- 04 December 2018, e23
-
- Article
- Export citation
Efficiently Coupling the I-DLV Grounder with ASP Solvers
-
- Journal:
- Theory and Practice of Logic Programming / Volume 20 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 205-224
-
- Article
- Export citation
Q-Table compression for reinforcement learning
- Part of
-
- Journal:
- The Knowledge Engineering Review / Volume 33 / 2018
- Published online by Cambridge University Press:
- 04 December 2018, e22
-
- Article
- Export citation
UNIFICATION IN SUPERINTUITIONISTIC PREDICATE LOGICS AND ITS APPLICATIONS
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 37-61
- Print publication:
- March 2019
-
- Article
- Export citation
A survey of large-scale reasoning on the Web of data
-
- Journal:
- The Knowledge Engineering Review / Volume 33 / 2018
- Published online by Cambridge University Press:
- 03 December 2018, e21
-
- Article
- Export citation
Filling Sound with Space: An elemental approach to sound spatialisation
-
- Journal:
- Organised Sound / Volume 23 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 296-307
- Print publication:
- December 2018
-
- Article
- Export citation
Theremin in the Press: Instrument remediation and code-instrument transduction
-
- Journal:
- Organised Sound / Volume 23 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 256-269
- Print publication:
- December 2018
-
- Article
- Export citation
Staging the Kinetic: How music automata sensitise audiences to sound art
-
- Journal:
- Organised Sound / Volume 23 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 235-245
- Print publication:
- December 2018
-
- Article
- Export citation
Editorial: Sound and kinetics – performance, artistic aims and techniques in electroacoustic music and sound art
-
- Journal:
- Organised Sound / Volume 23 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 219-224
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
OSO volume 23 issue 3 Cover and Front matter
-
- Journal:
- Organised Sound / Volume 23 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. f1-f2
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation