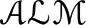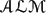Refine search
Actions for selected content:
48287 results in Computer Science
Anytime answer set optimization via unsatisfiable core shrinking
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 533-551
-
- Article
- Export citation
The dlvhex system for knowledge representation: recent advances (system description)*
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 866-883
-
- Article
- Export citation
Combining Answer Set Programming and domain heuristics for solving hard industrial problems (Application Paper)
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 653-669
-
- Article
- Export citation
First-order modular logic programs and their conservative extensions
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 755-770
-
- Article
- Export citation
Deriving conclusions from non-monotonic cause-effect relations*
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 670-687
-
- Article
- Export citation
On the Implementation of an Or-Parallel Prolog System for Clusters of Multicores
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 899-915
-
- Article
- Export citation
Iterative Learning of Answer Set Programs from Context Dependent Examples
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 834-848
-
- Article
- Export citation
CoreALMlib: An
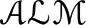 $\mathscr{ALM}$ library translated from the Component Library
$\mathscr{ALM}$ library translated from the Component Library
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 800-816
-
- Article
- Export citation
Inspiration choices that matter: the selection of external stimuli during ideation
-
- Journal:
- Design Science / Volume 2 / 2016
- Published online by Cambridge University Press:
- 14 October 2016, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logic Programming with Graph Automorphism: Integrating nauty with Prolog (Tool Description)*
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 688-702
-
- Article
- Export citation
A Physician Advisory System for Chronic Heart Failure management based on knowledge patterns
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 604-618
-
- Article
- Export citation
TLP volume 16 issue 5-6 Cover and Front matter
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation

Temporal Logics in Computer Science
- Finite-State Systems
-
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016
References
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 716-736
-
- Chapter
- Export citation
2 - Preliminaries and Background I
- from PART I - MODELS
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 17-34
-
- Chapter
- Export citation
12 - Frameworks for Decision Procedures
- from PART IV - METHODS
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 467-475
-
- Chapter
- Export citation
5 - Basic Modal Logics
- from PART II - LOGICS
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 100-149
-
- Chapter
- Export citation
8 - The Modal Mu-Calculus
- from PART II - LOGICS
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 271-328
-
- Chapter
- Export citation
NLE volume 22 issue 6 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 22 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 13 October 2016, pp. b1-b7
-
- Article
-
- You have access
- Export citation
9 - Alternating-Time Temporal Logics
- from PART II - LOGICS
-
- Book:
- Temporal Logics in Computer Science
- Published online:
- 13 October 2016
- Print publication:
- 13 October 2016, pp 329-358
-
- Chapter
- Export citation