Refine search
Actions for selected content:
25847 results in Abstract analysis
Homogeneous forms of odd degree in a large number of variables
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-105
- Print publication:
- December 1957
-
- Article
- Export citation
On the fractional parts of the powers of a rational number (II)
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
- Print publication:
- December 1957
-
- Article
- Export citation
On the solution of problems of dynamic plane elasticity
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 166-168
- Print publication:
- December 1957
-
- Article
- Export citation
An inversion formula for a generalized transform
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 146-155
- Print publication:
- December 1957
-
- Article
- Export citation
The distribution of quadratic residues and non-residues
-
- Journal:
- Mathematika / Volume 4 / Issue 2 / December 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
- Print publication:
- December 1957
-
- Article
- Export citation
Groups of order automorphisms of ordered sets
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-50
- Print publication:
- June 1957
-
- Article
- Export citation
Uniqueness theorems for thin clamped anisotropic plates
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 70-75
- Print publication:
- June 1957
-
- Article
- Export citation
Stress distribution in a notched plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-96
- Print publication:
- June 1957
-
- Article
- Export citation
A note on coverings
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1957
-
- Article
- Export citation
A note on form rings and ideals
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-60
- Print publication:
- June 1957
-
- Article
- Export citation
Bounded representations of integers by quadratic forms
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
- Print publication:
- June 1957
-
- Article
- Export citation
Multiple covering of the plane by circles
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-16
- Print publication:
- June 1957
-
- Article
- Export citation
A note on summability factors
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-40
- Print publication:
- June 1957
-
- Article
- Export citation
MTK volume 4 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
The Green's function of an elliptic plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-69
- Print publication:
- June 1957
-
- Article
- Export citation
XVIII.—Recent Oceanographical Investigations in the Faroe-Shetland Channel*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 239-289
- Print publication:
- 1957
-
- Article
- Export citation
XIX.—Metrisable Lie Groups and Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 290-304
- Print publication:
- 1957
-
- Article
- Export citation
XXI.—Index Polynomials and Bifurcating Root-Trees*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 319-341
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
XXIV.—Conditions for the Ergodicity of Non-homogeneous Finite Markov Chains*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 369-380
- Print publication:
- 1957
-
- Article
- Export citation
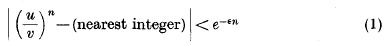
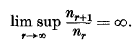
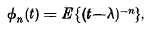
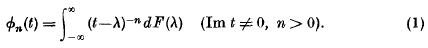
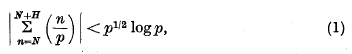
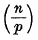 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.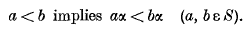

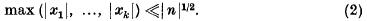
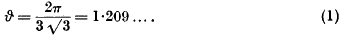
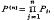 where
where 