Refine search
Actions for selected content:
25845 results in Abstract analysis
XXV.—The Determination of Temperature Gradients over the Greenland Ice Sheet by Optical Methods
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 381-397
- Print publication:
- 1957
-
- Article
- Export citation
XXIII. —Marine Research—The Work of the National Institute of Oceanography
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 350-368
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
XVII.—Invariant Matrices and the Geometry of Numbers
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 223-238
- Print publication:
- 1957
-
- Article
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 399-401
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
PRM volume 64 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
The spread of a matrix
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-130
- Print publication:
- December 1956
-
- Article
- Export citation
Dilational and distortional vibrations of semi-infinite solids and plates
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-163
- Print publication:
- December 1956
-
- Article
- Export citation
On a result of Marshall Hall
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-110
- Print publication:
- December 1956
-
- Article
- Export citation
MTK volume 3 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Note on irregularities of distribution
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-135
- Print publication:
- December 1956
-
- Article
- Export citation
Measurable almost periodic functions
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-143
- Print publication:
- December 1956
-
- Article
- Export citation
Indefinite quadratic forms in many variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-101
- Print publication:
- December 1956
-
- Article
- Export citation
Semi-regular local rings
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-126
- Print publication:
- December 1956
-
- Article
- Export citation
Thin circular plates under certain distributions of normal loading
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-152
- Print publication:
- December 1956
-
- Article
- Export citation
Extended computation of the Riemann zeta-function
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-108
- Print publication:
- December 1956
-
- Article
- Export citation
Indefinite quadratic polynomials in n variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-116
- Print publication:
- December 1956
-
- Article
- Export citation
Index to volume 3
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, p. 164
- Print publication:
- December 1956
-
- Article
- Export citation
Covering space by spheres
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-139
- Print publication:
- December 1956
-
- Article
- Export citation
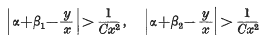
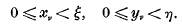
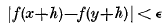
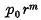 cos nϑ(or sin
cos nϑ(or sin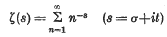
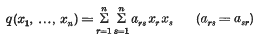
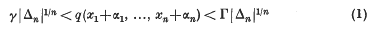
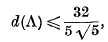
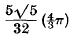 . Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.
. Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.