Refine search
Actions for selected content:
25845 results in Abstract analysis
Torsion of cylinders with inclusions*
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-103
- Print publication:
- June 1954
-
- Article
- Export citation
Index to volume 1
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 157
- Print publication:
- June 1954
-
- Article
- Export citation
A simple proof of η(— 1/τ)= η(τ)√τ/i
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 4
- Print publication:
- June 1954
-
- Article
- Export citation
Simultaneous Diophantine Approximation
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-72
- Print publication:
- June 1954
-
- Article
- Export citation
On convergence and summability factors in a sequence
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-44
- Print publication:
- June 1954
-
- Article
- Export citation
History of Science and Psychology of Invention
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1954
-
- Article
- Export citation
The minimal points of a positive definite quadratic form
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-17
- Print publication:
- June 1954
-
- Article
- Export citation
MTK volume 1 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1954
-
- Article
-
- You have access
- Export citation
The stability of an incompressible electrically conducting fluid rotating about an axis when current flows parallel to the axis
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-50
- Print publication:
- June 1954
-
- Article
- Export citation
The stability of viscous flow between rotating cylinders
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 5-13
- Print publication:
- June 1954
-
- Article
- Export citation
The Green's function of an elastic plate
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-23
- Print publication:
- June 1954
-
- Article
- Export citation
XIII.—A Statistical Examination of the Centroid Method*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 175-189
- Print publication:
- 1954
-
- Article
- Export citation
XVI.—Two Hologram Methods in Diffraction Microscopy
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 209-221
- Print publication:
- 1954
-
- Article
- Export citation
X.—A Configuration of Points and Spheres in Four-dimensional Space*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 145-149
- Print publication:
- 1954
-
- Article
- Export citation
IX.—On the Geometry of Ɛ-Matrices
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 127-144
- Print publication:
- 1954
-
- Article
- Export citation
XII.—On the Theory of Unimolecular Gas Reactions: A Quantum Harmonic Oscillator Model
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 161-174
- Print publication:
- 1954
-
- Article
- Export citation
XV.—Bounds for the Indices of Nilpotent and Solvable Lie Algebras*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 200-208
- Print publication:
- 1954
-
- Article
- Export citation
PRM volume 64 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1954
-
- Article
-
- You have access
- Export citation
VIII.—Riemann Extensions which have Kähler Metrics.
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 113-126
- Print publication:
- 1954
-
- Article
- Export citation
XI.—Theory of Indices for Non-Associative Algebra*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 150-160
- Print publication:
- 1954
-
- Article
- Export citation
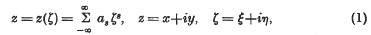
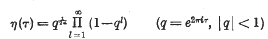
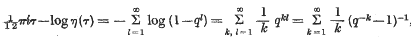
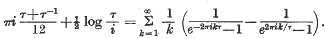
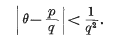

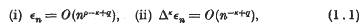
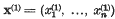 be a point at which this value is attained. Let
be a point at which this value is attained. Let 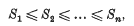

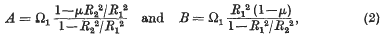

 at fixed temperature,
at fixed temperature, 