Refine search
Actions for selected content:
25847 results in Abstract analysis
VIII.—Riemann Extensions which have Kähler Metrics.
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 113-126
- Print publication:
- 1954
-
- Article
- Export citation
XI.—Theory of Indices for Non-Associative Algebra*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 150-160
- Print publication:
- 1954
-
- Article
- Export citation
XIV.—Studies in Practical Mathematics. VIII. On the Iterative Methods of Lin and Friedman for Factorizing Polynomials*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 2 / 1954
- Published online by Cambridge University Press:
- 14 February 2012, pp. 190-199
- Print publication:
- 1954
-
- Article
- Export citation
III.—The Problem of Two Bodies in Whitehead's Theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 49-56
- Print publication:
- 1953
-
- Article
- Export citation
I.—On Kuiper's Theory of the Origin of the Solar System*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-8
- Print publication:
- 1953
-
- Article
- Export citation
PRM volume 64 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1953
-
- Article
-
- You have access
- Export citation
V.—Interpolatory Methods for Theorems of Vitali and Montel Type*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 71-79
- Print publication:
- 1953
-
- Article
- Export citation
VII—Tidal Charts Based on Coastal Data: Irish Sea
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 90-111
- Print publication:
- 1953
-
- Article
- Export citation
VI.—The Maximum Term of an Entire Series
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 80-89
- Print publication:
- 1953
-
- Article
- Export citation
IV.—Expansion of a Finite One-dimensional Gas Cloud into a Vacuum*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 57-70
- Print publication:
- 1953
-
- Article
- Export citation
II.—Asymptotic Renewal Theorems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 1 / 1953
- Published online by Cambridge University Press:
- 14 February 2012, pp. 9-48
- Print publication:
- 1953
-
- Article
- Export citation
XIX.—A Generalization of the Classical Random-walk problem, and a Simple Model of Brownian Motion Based Thereon
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 268-279
- Print publication:
- 1952
-
- Article
- Export citation
XVIII.—The Elementary Proof of the Prime Number Theorem*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 257-267
- Print publication:
- 1952
-
- Article
- Export citation
XXIV.—The Solution of a Functional Equation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 336-345
- Print publication:
- 1952
-
- Article
- Export citation
XXVI.—The Normal Penetration of a Thin Elastic-Plastic Plate by a Right Circular Cone*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 359-370
- Print publication:
- 1952
-
- Article
- Export citation
XV.—Theorems on the Convergence and Asymptotic Validity of Abel's Series*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 222-231
- Print publication:
- 1952
-
- Article
- Export citation
XXIX.—The First Chemical Society, the First Chemical Journal, and the Chemical Revolution (Part II)*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 385-400
- Print publication:
- 1952
-
- Article
- Export citation
XXII.—Artificial Holograms and Astigmatism*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 313-323
- Print publication:
- 1952
-
- Article
- Export citation
XXVII.—The Rotational Field behind a Bow Shock Wave in Axially Symmetric Flow using Relaxation Methods*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 371-380
- Print publication:
- 1952
-
- Article
- Export citation
XX.—On the Estimation of Variance and Covariance
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 280-289
- Print publication:
- 1952
-
- Article
- Export citation
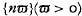 it is termed a
it is termed a 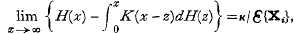
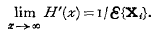
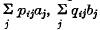 respectively. The
respectively. The 