Refine search
Actions for selected content:
25827 results in Abstract analysis
XXXVIII.—On the Estimation of Many Statistical Parameters
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 369-377
- Print publication:
- 1948
-
- Article
- Export citation
PRM volume 62 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1948
-
- Article
-
- You have access
- Export citation
XXXV.—Graphite Crystals and Crystallites. I. Binding Energies in Small Crystal Layers
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 336-349
- Print publication:
- 1948
-
- Article
- Export citation
XXXIV.—Foundations of Relativity: Parts I and II
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 319-335
- Print publication:
- 1948
-
- Article
- Export citation
XXIX.—On a Problem in Correlated Errors
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 273-277
- Print publication:
- 1948
-
- Article
- Export citation
XXVI.—The Universal Integral Invariants of Hamiltonian Systems and Application to the Theory of Canonical Transformations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 3 / 1948
- Published online by Cambridge University Press:
- 14 February 2012, pp. 237-246
- Print publication:
- 1948
-
- Article
- Export citation
XXIII.—The Number of the Elements
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 211-220
- Print publication:
- 1946
-
- Article
- Export citation
XVI.—Studies in Practical Mathematics. IV. On Linear Approximation by Least Squares
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 138-146
- Print publication:
- 1946
-
- Article
- Export citation
XXII.—Two Numerical Applications of Chebyshev Polynomials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 204-210
- Print publication:
- 1946
-
- Article
- Export citation
PRM volume 62 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f5
- Print publication:
- 1946
-
- Article
-
- You have access
- Export citation
XVIII.—The Riemann Tensor in a Completely Harmonic V4
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 156-163
- Print publication:
- 1946
-
- Article
- Export citation
XXI.—Tables of Chebyshev Polynomials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 187-203
- Print publication:
- 1946
-
- Article
- Export citation
XX.—Evaluation and Application of Certain Ladder-Type Networks
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 175-186
- Print publication:
- 1946
-
- Article
- Export citation
XIX.—A Theory of Regraduation in General Relativity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 164-174
- Print publication:
- 1946
-
- Article
- Export citation
XXIV.—Time-Scales in Relativity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 221-228
- Print publication:
- 1946
-
- Article
- Export citation
XIV.—On Substitutional Equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 117-126
- Print publication:
- 1946
-
- Article
- Export citation
XV.—Quantum Mechanics of Fields. III. Electromagnetic Field and Electron Field in Interaction
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 127-137
- Print publication:
- 1946
-
- Article
- Export citation
PRM volume 62 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1946
-
- Article
-
- You have access
- Export citation
XVII.—The Regraduation of Clocks in Spherically Symmetric Space-times of General Relativity.
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 2 / 1946
- Published online by Cambridge University Press:
- 14 February 2012, pp. 147-155
- Print publication:
- 1946
-
- Article
- Export citation
XIII.—A Problem in the Random Distribution of Particles
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 1 / 1944
- Published online by Cambridge University Press:
- 14 February 2012, pp. 103-115
- Print publication:
- 1944
-
- Article
- Export citation
 is (
is (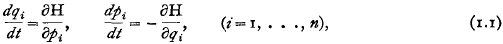
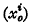 is a fixed point of a Riemannian V
is a fixed point of a Riemannian V
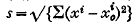 and
and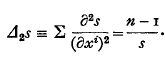
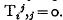 There are two alternatives, and regraduations are found to be excluded by one, the “geodesic” theory, but not necessarily by the other, the “equivalence” theory.
There are two alternatives, and regraduations are found to be excluded by one, the “geodesic” theory, but not necessarily by the other, the “equivalence” theory.