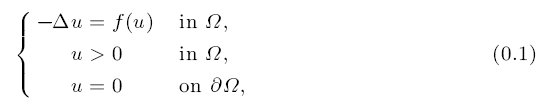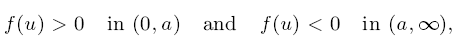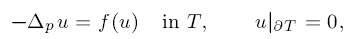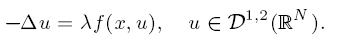Refine search
Actions for selected content:
25847 results in Abstract analysis
Non-classical global solutions for a class of scalar conservation laws
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 225-240
- Print publication:
- April 2004
-
- Article
- Export citation
Global and exponential attractors for nonlinear reaction–diffusion systems in unbounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 271-315
- Print publication:
- April 2004
-
- Article
- Export citation
Non-zero solutions for a Schrödinger equation with indefinite linear and nonlinear terms
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 249-258
- Print publication:
- April 2004
-
- Article
- Export citation
On a singularly perturbed wave equation with dynamic boundary conditions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 389-413
- Print publication:
- April 2004
-
- Article
- Export citation
A counterexample in Sturm–Liouville completeness theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 241-248
- Print publication:
- April 2004
-
- Article
- Export citation
DE RHAM–WITT COHOMOLOGY FOR A PROPER AND SMOOTH MORPHISM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 3 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 28 April 2004, pp. 231-314
- Print publication:
- April 2004
-
- Article
- Export citation
THE mKdV EQUATION ON THE HALF-LINE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 3 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 30 April 2004, pp. 139-164
- Print publication:
- April 2004
-
- Article
- Export citation
Umbilicity of space-like submanifolds of Minkowski space
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 375-387
- Print publication:
- April 2004
-
- Article
- Export citation
Strict convexity of level sets of solutions of some nonlinear elliptic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 363-373
- Print publication:
- April 2004
-
- Article
- Export citation
Symmetry for elliptic equations in a half-space without strong maximum principle
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 259-269
- Print publication:
- April 2004
-
- Article
- Export citation
Some elliptic semilinear indefinite problems on RN
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 333-361
- Print publication:
- April 2004
-
- Article
- Export citation
A CONVERSE TO MAZUR’S INEQUALITY FOR SPLIT CLASSICAL GROUPS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 3 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 28 April 2004, pp. 165-183
- Print publication:
- April 2004
-
- Article
- Export citation
Some remarks on thin operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 317-331
- Print publication:
- April 2004
-
- Article
- Export citation
4 - Stability and stabilization
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 63-88
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 151-161
-
- Chapter
- Export citation
5 - Spaces of persistent signals
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 89-120
-
- Chapter
- Export citation
Preface
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp vii-x
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 162-166
-
- Chapter
- Export citation
6 - Delay systems
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 121-150
-
- Chapter
- Export citation