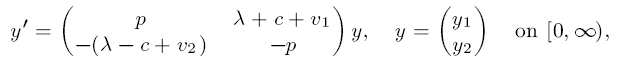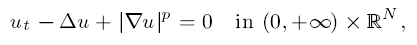Refine search
Actions for selected content:
25847 results in Abstract analysis
Contents
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp v-vi
-
- Chapter
- Export citation
1 - Operators and Hardy spaces
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 1-16
-
- Chapter
- Export citation
3 - Shift-invariance and causality
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 37-62
-
- Chapter
- Export citation
2 - Closed operators
-
- Book:
- Linear Operators and Linear Systems
- Published online:
- 07 May 2010
- Print publication:
- 15 March 2004, pp 17-36
-
- Chapter
- Export citation
Isoperimetric Problems for r-sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 277-279
-
- Article
- Export citation
Three Sampling Formulas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 185-193
-
- Article
- Export citation
A Note on a Question of Erdős and Graham
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 263-267
-
- Article
- Export citation
A Disproof of the Fon-der-Flaass Conjecture
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 195-201
-
- Article
- Export citation
Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry, by J Matoušek, Springer, 2003, 196 pp., £30.50/$49.95 €49.95
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 281-282
-
- Article
- Export citation
Point–Line Incidences in Space
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 203-220
-
- Article
- Export citation
Chromatic Roots are Dense in the Whole Complex Plane
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 221-261
-
- Article
- Export citation
A Subset Expansion of the Coloured Tutte Polynomial
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 269-275
-
- Article
- Export citation
On Phase Transition in the Hard-Core Model on ${\mathbb Z}^d$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 137-164
-
- Article
- Export citation
Distributed Colouring and Communication in Rings with Local Knowledge
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 123-136
-
- Article
- Export citation
On the Number of Edges in Random Planar Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 03 March 2004, pp. 165-183
-
- Article
- Export citation
On the use of Hadamard expansions in hyperasymptotic evaluation: differential equations of hypergeometric type
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 159-178
- Print publication:
- February 2004
-
- Article
- Export citation
Connection formulae for spectral functions associated with singular Dirac equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 215-223
- Print publication:
- February 2004
-
- Article
- Export citation
Very singular solutions to a nonlinear parabolic equation with absorption II. Uniqueness
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 39-54
- Print publication:
- February 2004
-
- Article
- Export citation
Bouncing solutions of an equation with attractive singularity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 201-213
- Print publication:
- February 2004
-
- Article
- Export citation
An elliptic boundary problem involving a semi-definite weight
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 134 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 12 July 2007, pp. 109-136
- Print publication:
- February 2004
-
- Article
- Export citation