Refine search
Actions for selected content:
25816 results in Abstract analysis
Prime and maximal ideals in polynomial rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 351-362
- Print publication:
- September 1995
-
- Article
-
- You have access
- Export citation
An integral formula for hypersurfaces in space forms
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 337-341
- Print publication:
- September 1995
-
- Article
-
- You have access
- Export citation
Finite groups generated by subnormal T-subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 363-371
- Print publication:
- September 1995
-
- Article
-
- You have access
- Export citation
Algebras of bounded finite dimensional representation type
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 289-302
- Print publication:
- September 1995
-
- Article
-
- You have access
- Export citation
Standard prime ideals and lying over for finite extensions of Noetherian algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 311-326
- Print publication:
- September 1995
-
- Article
-
- You have access
- Export citation
2 - Asymptotic Efficiency of Nonparametric Goodness-of-Fit Tests
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 40-93
-
- Chapter
- Export citation
3 - Asymptotic Efficiency of Nonparametric Homogeneity Tests
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 94-126
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp v-viii
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 249-264
-
- Chapter
- Export citation
Index
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 265-274
-
- Chapter
- Export citation
4 - Asymptotic Efficiency of Nonparametric Symmetry Tests
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 127-168
-
- Chapter
- Export citation
1 - Asymptotic Efficiency of Statistical Tests and Mathematical Means for Its Computation
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 1-39
-
- Chapter
- Export citation
5 - Asymptotic Efficiency of Nonparametric Independence Tests
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 169-207
-
- Chapter
- Export citation
Introduction
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp ix-xvi
-
- Chapter
- Export citation
6 - Local Asymptotic Optimality of Nonparametric Tests and the Characterization of Distributions
-
- Book:
- Asymptotic Efficiency of Nonparametric Tests
- Published online:
- 18 September 2009
- Print publication:
- 30 June 1995, pp 208-248
-
- Chapter
- Export citation
The value set of polynomials over ℤm and the combinatorics of sequences
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-198
- Print publication:
- June 1995
-
- Article
- Export citation
Inherited group actions on ℝ-trees
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 206-213
- Print publication:
- June 1995
-
- Article
- Export citation
M. Auslander, I. Reiten and S. O. Smalø. Representation Theory of Artin Algebras. Cambridge University Press. 1995, ISBN 0 521 41134 3, 423 pp., £50. - M. J. Baines. Moving Finite Elements. Clarendon Press. 1994, ISBN 0 19 853467 1, 226 pp., £45. - F. Borceux. Handbook of Categorical Algebra, I. Basic Category Theory. II. Categories and Structures. Encyclopedia of Mathematics and its Applications, 50, 51. Cambridge University Press. 1994, Vol. I, ISBN 0 521 44178 1, Vol. II, ISBN 0 521 44179 X, 345 pp., 443 pp., £45, £50. - H. J. M. Bos. Lectures in the History of Mathematics. AMS/LMS. 1993, ISBN 0 8218 9001 8, 197 pp., £71. - P. M. Cohn. Elements of Linear Algebra. Chapman and Hall. 1994, ISBN 0 412 55280 9, 226 pp., paperback, £13·99. - J. Dauns. Modules and Rings. Cambridge University Press. 1994, ISBN 0 521 46258 4, 442 pp., £45. - W. Dunham. The Mathematical Universe. Wiley. 1994, ISBN 0 471 53656 3, 314 pp., £16·95. - N. D. Gilbert and T. Porter. Knots and Surfaces. Oxford University Press. 1994, ISBN 0 19 853397 7, 268 pp., £29·50. - P. Griffiths and J. Harris. Principles of Algebraic Geometry. Wiley. 1994, ISBN 0 471 05059 8, 813 pp., £30·50. - W. K. Hayman. Multivalent Functions, 2nd Ed., Cambridge Tracts in Mathematics, Vol. 110. Cambridge University Press. 1994, ISBN 0 521 46026 3, 263 pp., £35. - W. V. D. Hodge and D. Pedoe. Methods of Algebraic Geometry, Vol. 1. Cambridge University Press. 1994, ISBN 0 521 469007 4, 440 pp., paperback, £14·95. - K. W. Morton and D. F. Mayers. Numerical Solution of Partial Differential Equations. Cambridge University Press. 1994, hardback ISBN 0 521 418550 0, paperback ISBN 0 521 42922 6, 227 pp., hardback, £35, paperback, £13·95. - J. D. Murray. Mathematical Biology, 2nd Ed. Springer. 1993, ISBN 3 540 57204 X, 767 pp., DM 68. - K. Nomizu and T. Sasaki. Affine differential Geometry. Cambridge University Press. 1994, ISBN 0 521 44177 3, 263 pp., £35. - J.-P. Pier, Editor. Development of Mathematics, 1900–1950. Birkhäuser. 1994, ISBN 3 7643 2821 5, 729 pp., £43. - M. Rahman. Water Waves. Relating Modern Theory to Advanced Engineering Practice. Clarendon Press. 1994, ISBN 0 19 853478 7, 343 pp., £50. - M. Rosenblum and J. Rovnyak. Topics in Hardy Classes and Univalent Functions. Birkhaüser. 1994, ISBN 3 7643 5111 X, 250 pp., £36. - I. R. Shafarevich. Basic Algebraic Geometry. Vol. I, Varieties in Projective Space. Vol. II, Schemes and Complex Manifolds. Springer. 1994, Vol. I, ISBN 3 540 54812 2, 303 pp., 68 DM, Vol. II, ISBN 3 540 57554 5, 269 pp., 68 DM. - D. Stoyan and H. Stoyan. Fractals, Random Shapes and Point Fields. Wiley. 1994, ISBN 0 471 93757 6, 389 pp., £39·95. - K. R. Stromberg. Probability for Analysts. Chapman and Hall. 1994, ISBN 0 412 04171 5, 330 pp., £49. - R. Torretti. Philosophy of geometry from Riemann to Poincaré. Reidel. 1994, ISBN 9 027 70920 3, 459 pp., £34. - N. J. Vilenkin and A. U. Klimyk. Representation of Lie Groups and Special Functions. Vol. 2, Class I Representations, Special Functions and Integral Transforms. Kluwer. 1993, ISBN 0 7923 1492 1, 607 pp., £183. - S. Zdravkovska and P. L. Duren, Editors. Golden Years of Moscow Mathematics. AMS/LMS. 1993, ISBN 0 8218 9003 4, 271 pp., £78.
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 222-227
- Print publication:
- June 1995
-
- Article
- Export citation
A note on Stokes flow due to a line rotlet
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
- Print publication:
- June 1995
-
- Article
- Export citation
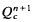 be an
be an 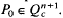 We consider the function
We consider the function 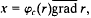 where
where 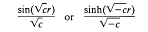
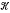 the class of finite groups that can be generated by subnormal
the class of finite groups that can be generated by subnormal 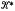 the subclass of
the subclass of 