Refine search
Actions for selected content:
25816 results in Abstract analysis
A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-157
- Print publication:
- June 1995
-
- Article
- Export citation
Unions of products of independent sets
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
- Print publication:
- June 1995
-
- Article
- Export citation
Chapter 3 - Rings of differential operators
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 20-25
-
- Chapter
- Export citation
Contents
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp vii-x
-
- Chapter
- Export citation
Chapter 18 - Preservation of holonomy
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 162-170
-
- Chapter
- Export citation
References
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 197-202
-
- Chapter
- Export citation
Coda
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 188-190
-
- Chapter
- Export citation
Appendix 1 - Defining the action of a module using generators
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 191-193
-
- Chapter
- Export citation
Chapter 1 - The Weyl algebra
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 8-13
-
- Chapter
- Export citation
Chapter 4 - Jacobian Conjecture
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 26-35
-
- Chapter
- Export citation
Chapter 11 - Characteristic varieties
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 97-107
-
- Chapter
- Export citation
Introduction
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 1-7
-
- Chapter
- Export citation
Chapter 6 - Differential equations
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 44-52
-
- Chapter
- Export citation
Preface
-
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp xi-xii
-
- Chapter
- Export citation
Chapter 12 - Tensor products
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 108-120
-
- Chapter
- Export citation
Chapter 7 - Graded and filtered modules
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 53-64
-
- Chapter
- Export citation
Chapter 16 - Direct images
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 146-153
-
- Chapter
- Export citation
Chapter 8 - Noetherian rings and modules
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 65-73
-
- Chapter
- Export citation
Chapter 19 - Stability of differential equations
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 171-178
-
- Chapter
- Export citation
Chapter 13 - External products
-
- Book:
- A Primer of Algebraic D-Modules
- Published online:
- 29 December 2009
- Print publication:
- 29 May 1995, pp 121-129
-
- Chapter
- Export citation
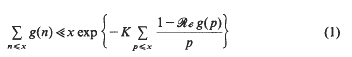
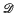 for all primes
for all primes 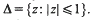 Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit
Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit 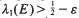 and
and 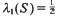 and
and 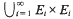 where the sets
where the sets 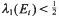 . The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.
. The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.