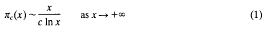Refine search
Actions for selected content:
25816 results in Abstract analysis
Skew group rings and maximal orders
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-263
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
A Mayer-Vietoris sequence in group homology and the decomposition of relation modules
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-171
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Polynomial Grothendieck properties
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 211-219
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Injective homogeneity and the Auslander–Gorenstein property
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 191-204
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Singular pleated surfaces and CP1–structures
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 179-190
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Primes of the form [pc] and related questions
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-141
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
On group graded rings satisfying polynomial identities
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 205-210
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Null 2-type Chen surfaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-242
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Minimum topological genus of compact bordered Klein surfaces admitting a prime-power automorphism
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-232
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
On the endomorphism semigroup of an ordered set
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-178
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Right fully idempotent rings need not be left fully idempotent
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 155-157
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Outer automorphisms of hypercentral p-groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 243-247
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
GMJ volume 37 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
7 - Lipschitz maps
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 100-108
-
- Chapter
- Export citation
18 - Rectifiability and orthogonal projections
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 250-264
-
- Chapter
- Export citation
19 - Rectifiability and analytic capacity in the complex plane
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 265-280
-
- Chapter
- Export citation
15 - Rectifiable sets and approximate tangent planes
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 202-219
-
- Chapter
- Export citation
1 - General measure theory
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 7-22
-
- Chapter
- Export citation
10 - Intersections with planes
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 139-145
-
- Chapter
- Export citation
4 - Hausdorff measures and dimension
-
- Book:
- Geometry of Sets and Measures in Euclidean Spaces
- Published online:
- 05 August 2012
- Print publication:
- 28 April 1995, pp 54-74
-
- Chapter
- Export citation
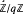 /q for any non-negative integer
/q for any non-negative integer  (
(
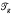 be the Teichmuller space of
be the Teichmuller space of 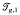 the space of marked hyperbolic structures on
the space of marked hyperbolic structures on