Refine search
Actions for selected content:
9019 results in Discrete Mathematics, Information Theory and Coding
Irreducible and end type group actions on Λ-trees
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-70
- Print publication:
- June 2002
-
- Article
- Export citation
On integers which are not differences of two powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-243
- Print publication:
- June 2002
-
- Article
- Export citation
Multiplicities of eigenvalues of a vector-valued Sturm-Liouville problem
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-127
- Print publication:
- June 2002
-
- Article
- Export citation
Hilbert function and fractional powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-75
- Print publication:
- June 2002
-
- Article
- Export citation
On the representation of an integer as the sum of a large and a small square
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-251
- Print publication:
- June 2002
-
- Article
- Export citation
Index to Volume 49
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, p. 263
- Print publication:
- June 2002
-
- Article
- Export citation
Rational homology of spaces of complex monic polynomials with multiple roots
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-91
- Print publication:
- June 2002
-
- Article
- Export citation
An analogue of Van der Corput's A5-process for exponential sums
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-183
- Print publication:
- June 2002
-
- Article
- Export citation
Small positive values of indefinite ternary forms
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-196
- Print publication:
- June 2002
-
- Article
- Export citation
The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
- Print publication:
- June 2002
-
- Article
- Export citation
Local inversion for differentiable functions and the Darboux property
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-158
- Print publication:
- June 2002
-
- Article
- Export citation
Lipschitz quotient mappings with good ratio of constants
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-165
- Print publication:
- June 2002
-
- Article
- Export citation
MTK volume 49 issue 1-2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
On shifted products which are powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-230
- Print publication:
- June 2002
-
- Article
- Export citation
Uniqueness theorems for convex bodies in non-Euclidean spaces
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-31
- Print publication:
- June 2002
-
- Article
- Export citation
Book Reviews - T. Andreescu and Z. Feng (editors). Mathematical Olympiads: Problems and Solutions from around the World. Mathematical Association of America: (1998–1999) 2000, 290 pp., ISBN 0 88385 803 7 (paperback), £19.95; (1999–2000) 2002, 323 pp., ISBN 0 88385 805 3 (paperback), £21.95. - K. Bichteler. Stochastic Integration with Jumps. Encyclopedia of Mathematics and its Applications 89, Cambridge University Press, 2002; 501 pp. ISBN 0 52181129 5 (hardback), £70. - K. Binmore and J. Davies. Calculus: Concepts and Methods. Cambridge University Press, 2001; 554 pp. ISBN 0 521 77541 8 (paperback), £25.95. - P. M. Bleher and A. R. Its (editors). Random Matrix Models and their Applications. MSRI Publications 40, Cambridge University Press, 2001; 438 pp. ISBN 0 521 80209 1 (hardback), £45. - E. Bujalance. A. F. Costa and E. Martinez. Topics on Riemann Surfaces and Fuchsian Groups. London Mathematical Society Lecture Notes Series 287, Cambridge University Press, 2001; 177 pp. ISBN 0521003504 (paperback). £24.95. - R. Churchhouse. Codes and Ciphers. Cambridge University Press. 2002; 240 pp. ISBN 052181054X (hardback), £40; 0521008905 (paperback). £14.95. - I. B. Cohen and G. E. Smith (editors). The Cambridge Companion to Newton. Cambridge University Press, 2002; 500 pp. ISBN 0 52165696 6 (paperback), £15.95. - E. Cumberbatch and A. Fitt (editors). Mathematical Modeling: Case Studies from Industry. Cambridge University Press, 2001; 299 pp. ISBN 0 52165007 0 (hardback), £65; 0 521 01173 6 (paperback), £23.95. - B. A. Davey and H. A. Priestley. Introduction to Lattices and Order (2nd edition). Cambridge University Press, 2002; 298 pp. ISBN 0 521784514 (paperback), £19.95. - S. K. Donaldson. Floer Homology Groups in Yang-Mills Theory. Cambridge Tracts in Mathematics 147, Cambridge University Press, 2002; 236 pp. ISBN 0 521 80803 0 (hardback), £50. - P. G. Drazin. Introduction to Hydrodynamic Stability. Cambridge Texts in Applied Mathematics, Cambridge University Press, 2002; 258 pp. ISBN 0 521 80427 2 (hardback), £65; 0 52100965 0 (paperback), £21.95. - R. M. Dudley. Real Analysis and Probability. Cambridge Studies in Advanced Mathematics 74, Cambridge University Press, 2002; 555 pp. ISBN 0 521 80972 X (hardback), £90; 0 521 007542 (paperback), £32.95. - H. Edllsbrunner. Geometry and Topology for Mesh Generation. Cambridge Monographs on Applied and Computational Mathematics 6, Cambridge University Press, 2001; 177 pp. ISBN 0 521 79309 2 (hardback), £29.95. - J. Eels and B. Fuglede. Harmonic Maps between Riemannian Polyhedra. Cambridge Tracts in Mathematics 142, Cambridge University Press, 2001; 296 pp. ISBN 0 521 77311 3 (hardback), £40. - J. F. Epperson. An Introduction to Numerical Methods and Analysis. John Wiley and Sons (New York), 2002; 556 pp. ISBN 0471 31647 4 (hardback). £32.50. - G. R. Fulford and P. Broadbridge. Industrial Mathematics: Case Studies in the Diffusion of Heat and Matter. Australian Mathematical Society Lecture Series 16, Cambridge University Press, 2002; 202 pp. ISBN 0521807174 (hardback), £47.50; 052100181 1 (paperback), £17.95. - W. J. Gilbert. Modern Algebra with Applications. Wiley-lnterscience Publication, John Wiley and Sons (New York), 2002; 348 pp. ISBN 0471 29891 3 (hardback), £112; 0471 23543 1 (paperback), £59.50. - J. E. Graver. Counting on Frameworks. The Dolciani Mathematical Expositions 25, Mathematical Association of America, 2001; 180 pp. ISBN 0 883 85331 0 (paperback), £23.95. - O. Haggstrom. Finite Markov Chains and Algorithmic Applications. London Mathematical Society Student Texts 32, Cambridge University Press, 2002; 114 pp. ISBN 0 52181357 3 (hardback), £40; 0 521890012 (paperback), £14.95. - A. Hatcher. Algebraic Toplogy. Cambridge University Press, 2002; 544 pp. ISBN 0521 79160X (hardback), £60; 0521 795400 (paperback), £20.95. - A. A. Ivanov and S. V. Shpectorov. Geometry of Sporadic Groups, II: Representations and Amalgams. Encyclopedia of Mathematics and its Applications 91, Cambridge University Press, 2002; 286 pp. ISBN 0 521 623499 (hardback), £50. - G. D. James and M. Liebeck. Representations and Characters of Groups (2nd edition). Cambridge University Press, 2001; 458 pp. ISBN 0 521 81205 4 (hardback), £80; 0 521 00392 X (paperback), £24.95. - Y. K. Kwok. Applied Complex Variables for Scientists and Engineers. Cambridge University Press, 2002; 392 pp. ISBN 0 521 004624 (paperback), £19.95. - A. Liu (editor). Hungarian Problem Book III: Based on the Eötvös Competitions, 1929–1943. The Anneli Lax New Mathematical Library 42. Mathematical Association of America, 2001; 142 pp. ISBN 0 88385 644 1 (paperback), £20.95. - M. Lothaire. Algebraic Combinatorics on Words. Encyclopedia of Mathematics and its Applications 90, Cambridge University Press, 2002; 504 pp. ISBN 0 521 81220 8 (hardback), £60. - P. Lounesto. Clifford Algebras and Spinors (2nd edition). London Mathematical Society Lecture Notes Series 286, Cambridge University Press. 2001; 338 pp. ISBN 0 521 00551 5 (paperback), £29.95. - J. Mccleary. A User's guide to Spectral Sequences (2nd edition. Cambridge Studies in Advanced Mathematics 58, Cambridge University Press, 2001; 561 pp. ISBN 0 521561418 (hardback), £60; 0 52156759 9 (paperback), £21.95. - R. J. Mceliece. The Theory of Information and Coding (2nd edition). Encyclopedia of Mathematics and its Applications 86, Cambridge University Press, 2002; 397 pp. ISBN0521 00095 5 (hardback), £60. - G. W. Milton. The Theory of Composites. Cambridge Monographs on Applied and Computational Mathematics 6, Cambridge University Press, 2002; 719 pp. ISBN 0 521 78125 6 (hardback), £60. - S. Montgomery and H. J. Schneider (editors). New Directions in Hopf Algebras. MSRI Publications 43, Cambridge University Press, 2002; 485 pp. ISBN 0 521 81512 6 (hardback), £55. - D. Mumford, C. Series and D. Wright. Indra's Pearls: The Vision of Felix Klein. Cambridge University Press, 2002; 396 pp. ISBN0 521 35253 3 (hardback), £29.95. - A. Neumaier. Introduction to Numerical Analysis. Cambridge University Press. 2001; 356 pp. ISBN0 52133323 7 (hardback), £65; 0 521336104 (paperback). £23.95. - T. W. Palmer. Banach Algebras and the General Theory *-Algebras, Vol. II. Encyclopedia of Mathematics and its Applications 79, Cambridge University Press, 2001; 823 pp. ISBN 0 521 36638 0 (hardback), £75. - D. Pollard. A User's Guide to Measure-Theoretic Probability. Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, 2002; 351 pp. ISBN0 52180242 3 (hardback), £60; 0521002893 (paperback), £20.95. - B. Polster and G. Steinke. Geometries on Surfaces. Encyclopedia of Mathematics and its Applications 84, Cambridge University Press, 2001; 490 pp. ISBN 0 521 66058 0 (hardback), £65. - I. R. Porteous. Geometric Differentiation, for the Intelligence of Curves and Surfaces (2nd edition). Cambridge University Press, 2001; 333 pp. ISBN 0 521 81040 X (hardback), £70; 0 521 002648 (paperback), £24.95. - A. Pressley (editor). Quantum Groups and Lie Theory. London Mathematical Society Lecture Notes Series 290, Cambridge University Press. 2001; 234 pp. ISBN 0 521 01040 3 (paperback), £27.95. - J. Tanton. Solve This: Math. Activities for Students and Clubs. Classroom Resource Materials, Mathematical Association of America, 2001; 218 pp. ISBN0883857170 (paperback), £20.95. - H. Walser. The Golden Section (2nd edition). Spectrum Series, Mathematical Association of America, 2001; 142 pp. ISBN 0 88385 534 8 (paperback), £17.95. - D. Williams. Weighing the Odds: A Course in Probability and Statistics. Cambridge University Press, 2001; 547 pp. ISBN 0 521 80356 X (hardback), £70; 0 521 00618 X (paperback), £24.95. - G. WüStholz (editor). A Panorama in Number Theory or the View from Baker's Garden. Cambridge University Press, 2002; 356 pp. ISBN 0 521 80799 9 (hardback), £55.
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-261
- Print publication:
- June 2002
-
- Article
- Export citation
Quick asymptotic upper bounds for lattice kissing numbers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-57
- Print publication:
- June 2002
-
- Article
- Export citation
On the reverse Lp–busemann–petty centroid inequality
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
- Print publication:
- June 2002
-
- Article
- Export citation
On extensions generated by roots of lifting polynomials
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-118
- Print publication:
- June 2002
-
- Article
- Export citation
Absolute curvature measures for unions of sets with positive reach
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-44
- Print publication:
- June 2002
-
- Article
- Export citation

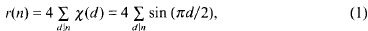

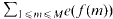 . The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].
. The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].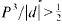 .
.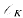 , the ring of integers of
, the ring of integers of 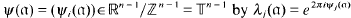 . Then the small region of
. Then the small region of 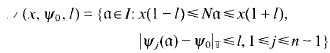
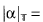 β. where β is the unique real satisyfing
β. where β is the unique real satisyfing 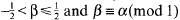 .
.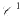 functions extends in finite dimension to everywhere differentiable functions. As usual, a theorem of implicit functions can be deduced from this “Local Inversion Theorem”. The deepest part of the local inversion theorem consists of showing that a differentiable function with non-vanishing Jacobian determinant is locally one-to-one. In turn, this fact allows one to extend the Darboux property of derivative functions on ℝ (the range of the derivative is an interval) to the Jacobian function
functions extends in finite dimension to everywhere differentiable functions. As usual, a theorem of implicit functions can be deduced from this “Local Inversion Theorem”. The deepest part of the local inversion theorem consists of showing that a differentiable function with non-vanishing Jacobian determinant is locally one-to-one. In turn, this fact allows one to extend the Darboux property of derivative functions on ℝ (the range of the derivative is an interval) to the Jacobian function 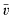 its unique prolongation to a fixed algebraic closure
its unique prolongation to a fixed algebraic closure 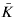 of
of 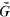 . For any subfield
. For any subfield 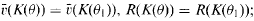 in case (
in case (