Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
Simple Matroids with Bounded Cocircuit Size
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 407-419
-
- Article
- Export citation
String Quartets in Binary
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 381-390
-
- Article
- Export citation
A Note on VC-Dimension and Measure of Sets of Reals
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 391-405
-
- Article
- Export citation
The Clairvoyant Demon Has a Hard Task
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 421-424
-
- Article
- Export citation
Discrete Isoperimetric Inequalities and the Probability of a Decoding Error
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 465-479
-
- Article
- Export citation
Propp–Wilson Algorithms and Finitary Codings for High Noise Markov Random Fields
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 5 / September 2000
- Published online by Cambridge University Press:
- 14 February 2001, pp. 425-439
-
- Article
- Export citation
New Radon–Nikodym ideals
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 219-227
- Print publication:
- December 2000
-
- Article
- Export citation
MTK volume 47 issue 1-2 Cover and Back matter
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
MTK volume 47 issue 1-2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-61
- Print publication:
- December 2000
-
- Article
- Export citation
A note on porosity and the Mazur intersection property
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-272
- Print publication:
- December 2000
-
- Article
- Export citation
Asymptotic lower bounds for Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-159
- Print publication:
- December 2000
-
- Article
- Export citation
The integral representation for a solution of the 2-d Dirichlet problem with boundary data on closed and open curves
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 339-354
- Print publication:
- December 2000
-
- Article
- Export citation
Parallelizable manifolds and the fundamental group
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-172
- Print publication:
- December 2000
-
- Article
- Export citation
Reconstruction of polytopes by convex pastings
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 9-18
- Print publication:
- December 2000
-
- Article
- Export citation
Scattering of tidal waves by reefs and spits
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 355-370
- Print publication:
- December 2000
-
- Article
- Export citation
Maximal sections and centrally symmetric bodies
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-30
- Print publication:
- December 2000
-
- Article
- Export citation
Inscribing cubes and covering by rhombic dodecahedra via equivariant topology
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 371-397
- Print publication:
- December 2000
-
- Article
- Export citation
Combinatorics and linear algebra of Freiman's isomorphism
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-51
- Print publication:
- December 2000
-
- Article
- Export citation
Lusternik-Schnirelmann category and Morse decompositions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 299-305
- Print publication:
- December 2000
-
- Article
- Export citation
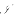 on
on 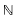 satisfy the following requirement: any measurable homomorphism
satisfy the following requirement: any measurable homomorphism 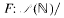
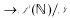 has a continuous lifting
has a continuous lifting 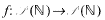 which is a homomorphism itself. Ideals having such a property were called
which is a homomorphism itself. Ideals having such a property were called 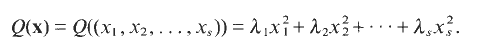
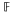 of convex sets, satisfying a given property P. Moreover, assume that
of convex sets, satisfying a given property P. Moreover, assume that  . As a consequence, it follows that, if all simplices or small enough simplices have the property in question, then
. As a consequence, it follows that, if all simplices or small enough simplices have the property in question, then 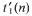 of classes of such cardinality
of classes of such cardinality 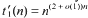 .
.