Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
Frequency of oscillations of an error term related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-164
- Print publication:
- December 2000
-
- Article
- Export citation
A functional analytic interpretation of the number of faces of a polyhedron
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-7
- Print publication:
- December 2000
-
- Article
- Export citation
Factorization over local fields and the irreducibility of generalized difference polynomials
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-196
- Print publication:
- December 2000
-
- Article
- Export citation
Un nouveau critère pour l'équation de Catalan
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-73
- Print publication:
- December 2000
-
- Article
- Export citation
The discrete fractional Fourier transform and Harper's equation
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-297
- Print publication:
- December 2000
-
- Article
- Export citation
Bounds for the points of spectral concentration of Sturm–Liouville problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 327-337
- Print publication:
- December 2000
-
- Article
- Export citation
The convexity of the spectral function in Sturm–Liouville problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-326
- Print publication:
- December 2000
-
- Article
- Export citation
N-fold sums of Cantor sets
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-250
- Print publication:
- December 2000
-
- Article
- Export citation
Character sums with exponential functions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-85
- Print publication:
- December 2000
-
- Article
- Export citation
The order of inverses mod q
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-108
- Print publication:
- December 2000
-
- Article
- Export citation
Index to volume 47
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 411-412
- Print publication:
- December 2000
-
- Article
- Export citation
The order of groups satisfying a converse to Lagrange's theorem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-204
- Print publication:
- December 2000
-
- Article
- Export citation
On properties of metrizable spaces X preserved by t-equivalence
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-279
- Print publication:
- December 2000
-
- Article
- Export citation
Density and covering properties of intervals of ℝn
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-242
- Print publication:
- December 2000
-
- Article
- Export citation
Bh [g] sequences
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- December 2000
-
- Article
- Export citation
Multiple solutions for semilinear elliptic problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 307-317
- Print publication:
- December 2000
-
- Article
- Export citation
Fubini-type theorems for general measure constructions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-265
- Print publication:
- December 2000
-
- Article
- Export citation
Segments in ball packings
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 31-38
- Print publication:
- December 2000
-
- Article
- Export citation
Additive representation in thin sequences, II: The binary Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-125
- Print publication:
- December 2000
-
- Article
- Export citation
Classes of integral 3-tensors on 2-space
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-217
- Print publication:
- December 2000
-
- Article
- Export citation
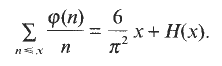
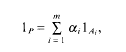


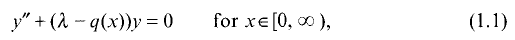
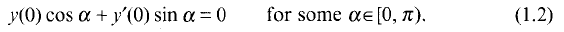
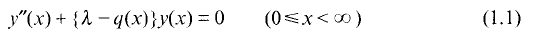
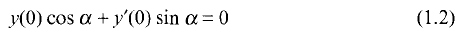
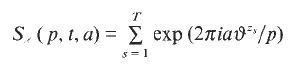
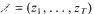 a sequence such that
a sequence such that 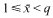 be such that
be such that 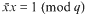 . For fixed
. For fixed 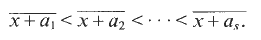
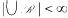 , then there is a finite sequence
, then there is a finite sequence 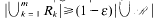 and
and 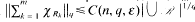 .
.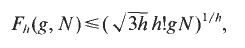
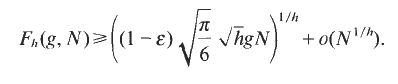
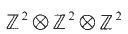 under the standard action of
under the standard action of 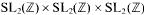 . A notion of primitivity is defined in this space and the number of primitive classes of a given discriminant is evaluated in terms of the class number of primitive binary quadratic forms of the same discriminant. Classes containing symmetric 3-tensors are also considered and their number is related to the 3-rank of the class group.
. A notion of primitivity is defined in this space and the number of primitive classes of a given discriminant is evaluated in terms of the class number of primitive binary quadratic forms of the same discriminant. Classes containing symmetric 3-tensors are also considered and their number is related to the 3-rank of the class group.