Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
Chapter I - The type problem
-
- Book:
- Random Walks on Infinite Graphs and Groups
- Published online:
- 22 September 2009
- Print publication:
- 13 February 2000, pp 1-80
-
- Chapter
- Export citation
Preface
-
- Book:
- Random Walks on Infinite Graphs and Groups
- Published online:
- 22 September 2009
- Print publication:
- 13 February 2000, pp viii-xii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Random Walks on Infinite Graphs and Groups
- Published online:
- 22 September 2009
- Print publication:
- 13 February 2000, pp i-iv
-
- Chapter
- Export citation
Chapter III - The asymptotic behaviour of transition probabilities
-
- Book:
- Random Walks on Infinite Graphs and Groups
- Published online:
- 22 September 2009
- Print publication:
- 13 February 2000, pp 139-219
-
- Chapter
- Export citation
Chapter IV - An introduction to topological boundary theory
-
- Book:
- Random Walks on Infinite Graphs and Groups
- Published online:
- 22 September 2009
- Print publication:
- 13 February 2000, pp 220-314
-
- Chapter
- Export citation
Random Star Processes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 33-43
-
- Article
- Export citation
The Choice Number of Dense Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 19-26
-
- Article
- Export citation
Bipartite Subgraphs and the Smallest Eigenvalue
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 1-12
-
- Article
- Export citation
A Note on Sequential Selection from Permutations
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 13-17
-
- Article
- Export citation
Proof of the Van den Berg–Kesten Conjecture
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 27-32
-
- Article
- Export citation
Algorithms for Colouring Random k-colourable Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 45-77
-
- Article
- Export citation
On the Choice Number of Random Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 79-95
-
- Article
- Export citation
On integers with identical digits
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 411-417
- Print publication:
- December 1999
-
- Article
- Export citation
On extending Artin's conjecture to composite moduli
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 373-390
- Print publication:
- December 1999
-
- Article
- Export citation
On the scarcity of powerful binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-410
- Print publication:
- December 1999
-
- Article
- Export citation
Index to Volume 46
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 477-478
- Print publication:
- December 1999
-
- Article
- Export citation
On the Steinhaus tiling problem
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-280
- Print publication:
- December 1999
-
- Article
- Export citation
Compact measure spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-336
- Print publication:
- December 1999
-
- Article
- Export citation
On the convergence of Σ∞n = 1f(nx) for measurable functions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-341
- Print publication:
- December 1999
-
- Article
- Export citation
Sign changes of error terms related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-395
- Print publication:
- December 1999
-
- Article
- Export citation
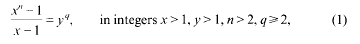
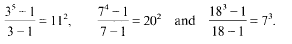
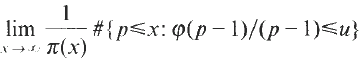
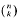 with 3≤
with 3≤ . Unconditionally, it is shown that there are
. Unconditionally, it is shown that there are