Refine search
Actions for selected content:
9017 results in Discrete Mathematics, Information Theory and Coding
Sums of k-th powers in number fields
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-370
- Print publication:
- December 1998
-
- Article
- Export citation
Simultaneous diagonal p–adic equations
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-349
- Print publication:
- December 1998
-
- Article
- Export citation
MTK volume 45 issue 2 Back matter
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
On simultaneous additive equations, IV
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-335
- Print publication:
- December 1998
-
- Article
- Export citation
On a Combinatorial Theorem of Erdös, Ginzburg and Ziv
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 403-412
-
- Article
- Export citation
Common Subsequences and Supersequences and their Expected Length
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 365-373
-
- Article
- Export citation
Nonlinear evolution of Rayleigh waves in an initial value context: non-symmetric input and cross-flow
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 217-243
- Print publication:
- December 1998
-
- Article
- Export citation
Minkowski sums of projections of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-268
- Print publication:
- December 1998
-
- Article
- Export citation
The Asymptotic Proportion of Subdivisions of a 2×2 Table that Result in Simpson's Paradox
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 387-396
-
- Article
- Export citation
Asymptotic Enumeration of Eulerian Circuits in the Complete Graph
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 437-449
-
- Article
- Export citation
Expected Value Expansions in Random Subgraphs with Applications to Network Reliability
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 465-483
-
- Article
- Export citation
On Vertex-Triads in 3-Connected Binary Matroids
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 485-497
-
- Article
- Export citation
Stability estimates for star bodies in terms of their intersection bodies
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-303
- Print publication:
- December 1998
-
- Article
- Export citation
The slices of a cone and a characterization of ellipsoids
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-317
- Print publication:
- December 1998
-
- Article
- Export citation
Concentration of the distance in finite dimensional normed spaces
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-252
- Print publication:
- December 1998
-
- Article
- Export citation
On a Conjecture of Bollobás and Brightwell Concerning Random Walks on Product Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 397-401
-
- Article
- Export citation
Uniquely Colourable Graphs and the Hardness of Colouring Graphs of Large Girth
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 375-386
-
- Article
- Export citation
M. Aigner and G. M. Ziegler. Proofs from THE BOOK. Springer-Verlag (Berlin, etc.), 1998. ISBN 3 540 63698 6; 199 pp., hardback, £19. - M. B. Allen and E. L. Isaacson. Numerical Analysis for Applied Science. Wiley–Interscience, 1998. ISBN 0 471 55266 6; 492 pp., hardback, £45·50. - A. S. Asratian, T. M. J. Denley and R. Häggkvist. Bipartite Graphs and their Applications. Cambridge University Press, 1998. ISBN 0 521 59345 X; 259 pp., hardback, £40. - S. Axler, J. E. McCarthy and D. Sarason, Editors. Holomorphic Spaces. Cambridge University Press, 1998. ISBN 0 521 63193 9; 476 pp., hardback, £35. - R. A. Bailey, Editor. Surveys in Combinatorics, 1997. Cambridge University Press, 1997. ISBN 0 521 59840 0; 338 pp., paperback, £24·95. - R. B. Bapat and T. E. S. Raghavan. Nonnegative Matrices and Applications. Encyclopedia of Mathematics and its Applications, Vol. 64, Cambridge University Press, 1997. ISBN 0 521 57167 7; 336 pp., hardback, £45. - D. J. Benson. Representations and Cohomology, Vols. I and II. Cambridge University Press, Vol. I, 1998, ISBN 0 521 63653 1; 246 pp., paperback, £18·95;. Vol. II, 1998, ISBN 0 521 63652 3, 267 pp., paperback, £18·95. - Jean Bertoin. Lévy Processes. Cambridge University Press, 1996. ISBN 0 521 56243 0; 265 pp., hardback, £35. - W. A. Coppel. Foundations of Convex Geometry. Cambridge University Press, 1998. ISBN 0 521 63970 0; 222 pp., paperback, £24·95. - R. Curtis and R. Wilson, Editors. The Atlas of Finite Groups: Ten Years on. London Mathematical Society Lecture Notes Series 249. Cambridge University Press, 1998. ISBN 0 521 57587 7; 293 pp., paperback, £27·95. - K. Engel. Sperner Theory. Cambridge University Press, 1997. ISBN 0 521 45206 6; 417 pp., hardback, £50. - K. Falconer. Fractal Geometry, Mathematical Foundations and Applications. Wiley-Interscience, 1997. ISBN 0 47196777 7; 288 pp., paperback, £14·99. Techniques in Fractal Geometry. Wiley-Interscience, 1997. ISBN 0 471 75724 0; 256 pp., paperback, £24·99. - R. Goodman and N. R. Wallach. Representations and Invariants of the Classical Groups, Encyclopedia of Mathematics and its Applications, Vol. 68. Cambridge University Press, 1998. ISBN 0 521 58273 3; 685 pp., hardback, £65. - J. Kollar and S. Mori. Birational Geometry of Algebraic Varieties. Cambridge Tracts in Mathematics 134. Cambridge University Press, 1998. ISBN 0 521 63277 3; 254 pp., hardback, £30. - V. S. Kulikov. Mixed Hodge Structures and Singularities. Cambridge University Press, 1998. ISBN 0 521 62060 0; 186 pp., hardback, £30. - P. C. Roberts. Multiplicities and Chern Classes in Local Algebra. Cambridge Tracts in Mathematics, 133. Cambridge University Press, 1998. ISBN 0 521 47316 0; 303 pp., hardback, £37·50. - F. Smithies. Cauchy and the Creation of Complex Function Theory. Cambridge University Press, 1997. ISBN 0 521 59278 X; 216 pp., hardback, £35. - R. P. Stanley. Enumerative Combinatorics, Vol. I. Cambridge University Press, 1997. ISBN 0 521 55309 1; 325 pp., hardback, £40. - E. Witt. Collected Papers, Editor I. Kersten. Springer-Verlag (Berlin, etc.), 1998. ISBN 3 540 57061 6; 420 pp., hardback, £76. - D. Zwillinger, Editor. CRC Standard Mathematical Tables and Formulae. CRC Press, 1996. ISBN 0 8493 2479 3; 812 pp., hardback, £29·50.
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-395
- Print publication:
- December 1998
-
- Article
- Export citation
Distant Vertex Partitions of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 413-422
-
- Article
- Export citation
Complexity and Probability of Some Boolean Formulas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 7 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 451-463
-
- Article
- Export citation
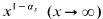 with
with 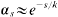 for large
for large 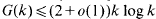 for large
for large 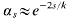 .
.