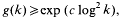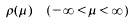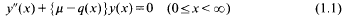Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
Hypergraph Packing and Graph Embedding
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 4 / July 1999
- Published online by Cambridge University Press:
- 01 July 1999, pp. 363-376
-
- Article
- Export citation
The Invited Lectures
-
- Book:
- Surveys in Combinatorics, 1999
- Published online:
- 05 May 2013
- Print publication:
- 01 July 1999, pp 15-16
-
- Chapter
- Export citation
On congruence compact monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-224
- Print publication:
- June 1999
-
- Article
- Export citation
On smooth gaps between consecutive prime numbers
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-75
- Print publication:
- June 1999
-
- Article
- Export citation
A density bound for efficient packings of 3-space with centrally symmetric convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-144
- Print publication:
- June 1999
-
- Article
- Export citation
A generalized fundamental principle
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
- Print publication:
- June 1999
-
- Article
- Export citation
Isotropic surface area measures
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic approximation of smooth convex bodies by general polytopes
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-125
- Print publication:
- June 1999
-
- Article
- Export citation
Bruce Blackadar. K-Theory for Operator Algebras (2nd edition). MSRI Publications 5. Cambridge University Press, 1998; 300 pp. ISBN 0 521 63532 2 (paperback), £19.95. - D. A. Brannan, M. E. Esplen and J. J. Gray. Geometry. Cambridge University Press, 1999; 497 pp. ISBN 0 521 59193 7 (hardback), £50; 0 521 59787 0 (paperback), £18.95. - W. Bruns and J. Herzog. Cohen-Macaulay Rings. Cambridge Studies in Advanced Mathematics 39. Cambridge University Press, 1998; 453 pp. ISBN 0 521 41068 1 (hardback), £55; 0 521 56674 6 (paperback), £24.95. - A. Bultheel, P. González-Vera, E. Hendriksen and O. Njåstad. Orthogonal Rational Functions. Cambridge University Press, 1999; 407 pp. ISBN 0 521 65006 2 (hardback), £37.50. - J. R. García Rozas. Covers and Envelopes in the Category of Complexes of Modules. CRC Research Notes in Mathematics 407. Chapman and Hall (Baton Rouge), 1999; 137 pp. ISBN 1 58488 004 X (paperback), £29.99. - Mariano Giaquinta and Stefan Hildebrandt. Calculus of Variations, I: the Lagrangian Formalism. Grundlehren der Mathematischen Wissenschaften 310. Springer-Verlag (Berlin), 1996; 475 pp. ISBN 3 540 50625 X (hardback), DM 188. Calculus of Variations, II: the Hamiltonian Formalism. Grundlehren der Mathematischen Wissenschaften 311. Springer-Verlag (Berlin), 1996; 652 pp. ISBN 3 540 57961 3 (hardback), DM 198. - C. G. Gibson. Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. Cambridge University Press, 1998; 250 pp. ISBN 0 521 64140 3 (hardback), £42.50; ISBN 0 521 64641 3 (paperback), £15.95. - Niccolo Guicciardini. Reading the Principia: The Debate on Newton's Mathematical Methods for Natural Philosophy from 1687 to 1736. Cambridge University Press, 1999; 285 pp. ISBN 0 521 64066 0 (hardback), £50. - Yoshiyuki Kitaoka. Arithmetic of Quadratic Forms. Cambridge Tracts in Mathematics 106. Cambridge University Press, 1999; 343 pp. ISBN 0 521 40475 4 (hardback), £50; 0 521 64996 X (paperback), £18.95. - Paul Koosis. Introduction to Hρ Spaces (2nd edition). Cambridge University Press, 1998; 287 pp. ISBN 0 521 45521 9 (hardback), £45. - S. Levy (Editor). The Eightfold Way: the Beauty of Klein's Quartic Curve. MSRI Publications 35. Cambridge University Press, 1999; 330 pp. ISBN 0 521 66066 1 (hardback), £35. - Pertti Mattila. Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability. Cambridge University Press, 1999; 344 pp. ISBN 0 521 46576 1 (hardback), £40; 0 521 65595 1 (paperback), £18.95. - Juan C. Migliore. Introduction to Liaison Theory and Deficiency Modules. Progress in Mathematics, Vol. 165. Birkhauser Verlag (Basel), 1998: 215 pp. ISBN 3 7643 4027 4 (hardback), £44. - Michael Monastyrsky. Modern Mathematics in the Light of the Fields Medals. A. K. Peters (Wellesley, Mass.), 1998; 160pp. ISBN 1 56881 083 0 (paperback), £12.50. - Mario Petrich and Norman R. Reilly. Completely Regular Semi-groups. Wiley (New York), 1999; 481pp. ISBN 0 471 19571 5 (hardback), £74.50. - Nigel P. Smart. The Algorithmic Resolution of Diophantine Equations. London Mathematical Society Student Texts 41. Cambridge University Press, 1998; 243 pp. ISBN 0 521 64156 X (hardback), £45; 0 52164633 2 (paperback), £16.95. - R. P. Stanley. Enumerative Combinatorics, Vol. 2. Cambridge University Press, 1999; 581 pp. ISBN 0 521 56069 1 (hardback), £45. - Paul Taylor. Practical Foundations of Mathematics. Cambridge Studies in Advanced Mathematics 59. Cambridge University Press, 1999; 572 pp. ISBN 0 521 63107 6 (hardback), £50. - Wang Yuan (Transl. Peter Shiu). Hua Loo-Keng: a Biography. Springer-Verlag (Singapore), 1999; 423 pp. ISBN 7 8077 415 5 (paperback), £22.50.
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-229
- Print publication:
- June 1999
-
- Article
- Export citation
A further generalization of Hilbert's inequality
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-39
- Print publication:
- June 1999
-
- Article
- Export citation
Kahane-Khinchine type inequalities for negative exponent
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-173
- Print publication:
- June 1999
-
- Article
- Export citation
Uniqueness of solutions to certain hyperbolic boundary value problems in a semi-infinite strip
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-163
- Print publication:
- June 1999
-
- Article
- Export citation
A Bernstein-type theorem in hyperbolic spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-81
- Print publication:
- June 1999
-
- Article
- Export citation
Maximal hyperplane sections of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-136
- Print publication:
- June 1999
-
- Article
- Export citation
On similar short sums
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-204
- Print publication:
- June 1999
-
- Article
- Export citation
Flatness properties of acts over commutative, cancellative monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
- Print publication:
- June 1999
-
- Article
- Export citation
Intersection bodies and polytopes
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-34
- Print publication:
- June 1999
-
- Article
- Export citation
Estimates of the least prime factor of a binomial coefficient
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-55
- Print publication:
- June 1999
-
- Article
- Export citation
On the location of spectral concentration for perturbed discrete spectra
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-154
- Print publication:
- June 1999
-
- Article
- Export citation
Convex bodies with non-convex cross-section bodies
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-129
- Print publication:
- June 1999
-
- Article
- Export citation
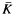 of
of 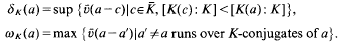
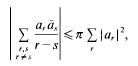
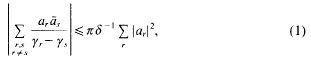


 are >
are >