Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
Rings which are residually ℤ
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-183
- Print publication:
- June 1999
-
- Article
- Export citation
MTK volume 46 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Non-vanishing of the partition function modulo odd primes l
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-192
- Print publication:
- June 1999
-
- Article
- Export citation
Convex intersection bodies in three and four dimensions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-27
- Print publication:
- June 1999
-
- Article
- Export citation
A Measure for the Non-Orthogonality of a Lattice Basis
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 281-291
-
- Article
- Export citation
Conditional Independences among Four Random Variables III: Final Conclusion
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 269-276
-
- Article
- Export citation
List Improper Colourings of Planar Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 293-299
-
- Article
- Export citation
On the Expected Depth of Random Circuits
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 209-228
-
- Article
- Export citation
On Increasing Subsequences of I.I.D. Samples
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 247-263
-
- Article
- Export citation
On the Structure of Dense Triangle-Free Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 237-245
-
- Article
- Export citation
On the Density of Universal Sum-Free Sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 277-280
-
- Article
- Export citation
On Systems of Small Sets with No Large Δ-Subsystems
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 265-268
-
- Article
- Export citation
On Poisson–Dirichlet Limits for Random Decomposable Combinatorial Structures
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 193-208
-
- Article
- Export citation
The Matroid Ramsey Number n(6,6)
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 3 / May 1999
- Published online by Cambridge University Press:
- 01 May 1999, pp. 229-235
-
- Article
- Export citation
7 - Symmetric Functions
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp 286-560
-
- Chapter
- Export citation
Notation
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp xi-xii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp 561-582
-
- Chapter
- Export citation
Additional Errata and Addenda
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp 583-585
-
- Chapter
- Export citation
6 - Algebraic, D-Finite, and Noncommutative Generating Functions
-
- Book:
- Enumerative Combinatorics
- Published online:
- 18 January 2010
- Print publication:
- 13 January 1999, pp 159-285
-
- Chapter
- Export citation
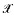 be a class of structures for a first-order language and let
be a class of structures for a first-order language and let