Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
Is there a different proof of the Erdős-Rado theorem?
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 27-38
-
- Chapter
- Export citation
Hypergraph games and the chromatic number
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 201-206
-
- Chapter
- Export citation
On graphs not containing prescribed induced subgraphs
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 111-120
-
- Chapter
- Export citation
Graphs with no unfriendly partitions
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 373-384
-
- Chapter
- Export citation
Partitions sans petits sommants
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 121-152
-
- Chapter
- Export citation
Large α-preserving sets in infinite α-connected graphs
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 445-450
-
- Chapter
- Export citation
Hamilton cycles in random graphs of minimal degree at least k
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 59-96
-
- Chapter
- Export citation
Sum-free subsets
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 13-26
-
- Chapter
- Export citation
On the greatest prime factor of an arithmetical progression
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 385-390
-
- Chapter
- Export citation
Some recent results on interpolation
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 451-458
-
- Chapter
- Export citation
A remark on heights of subspaces
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 359-360
-
- Chapter
- Export citation
On the mean convergence of derivatives of Lagrange interpolation
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 397-404
-
- Chapter
- Export citation
A Galvin–Hajnal conjecture on uncountably chromatic graphs
-
-
- Book:
- A Tribute to Paul Erdos
- Published online:
- 05 March 2012
- Print publication:
- 13 December 1990, pp 313-316
-
- Chapter
- Export citation
BOOK REVIEWS - D. J. Acheson. Elementary Fluid Dynamics. Clarendon Press. 1990, 397 pp., £15. - C. D. Aliprantis and O. Burkinshaw. Principles of Real Analysis. 2nd Edition. Academic Press. 1990, 295 pp., $39.95. - C. D. Aliprantis and O. Burkinshaw. Problems in Real Analysis. Academic Press. 1990, 285 pp., $29.95. - M. Aoki. Optimization of Stochastic Systems: Topics in Discrete-Time Dynamics. Academic Press. 1989, 417 pp., $64.95. - J. Borwein and P. Borwein. A Dictionary of Real Numbers. Wadsworth and Brooks/Cole. 1990, 424 pp., £55-50. - Y. A. Brychkov and A. P. Prudnikov. Integral Transforms of Generalized Functions. Gordon & Breach. 1989, 343 pp., $140. - A. J. Chorin. Computational Fluid Mechanics: Selected Papers. Academic Press. 1989, 223 pp., $35. - C. Clapham. The Concise Oxford Dictionary of Mathematics. Oxford University Press. 1990, 204 pp., £4-95. - P. Constantin and C. Foias. Navier-Stokes Equations. University of Chicago Press. 1988, 190 pp., £27-95. - S. Dineen. The Schwarz Lemma. Clarendon Press. 1989, 248 pp., £25. - P. Dita and V. Georgescu, Editors. Conformal Invariance and String Theory. Academic Press. 1989, 557 pp., $59.95. - L. Eldén and L. Wittmeyer-Koch. Numerical Analysis–an Introduction. Academic Press. 1990, 347 pp., $39.95. - K. D. Elworthy and J.-C. Zambrini. Stochastic Analysis, Path Integration and Dynamics. Longman. 1989, 263 pp., £18. - R. V. Gamkrelidze, Editor. Analysis I: Integral Representations and Asymptotic Methods. Springer. 1989, 238 pp., DM 128. - S. Gelbart and F. Shahidi. Analytic properties of automorphic L-functions. Academic Press. 1988, 131 pp., $18.75. - T. A. Grandine. The Numerical Methods Programming Projects Book. Oxford. 1990, 146 pp., £9-95 - M. H. J. Gruber. Regression Estimators: a Comparative Study. Academic Press. 1990, 347 pp., $49.95. - F. R. Harvey. Spinors and Calibrations. Academic Press. 1990, 313 pp., $39.95. - W. K. Hayman. Subharmonic Functions, Vol. 2. Academic Press. 1989, 590 pp., £53-50. - J. Kevorkian. Partial Differential Equations: Analytical Solution Techniques. Wadsworth and Brooks/Cole. 1990, 547 pp., £14-95. - H.-O. Kreiss and J. Lorenz. Initial-Boundary Value Problems and the Navier Stokes Equations. Academic Press. 1989, 402 pp., $54.50. - S. Lang. A First Course in Calculus. Fifth Edition. Springer. 1986, 280 pp., DM 128. - P. D. Lax and R. S. Phillips. Scattering Theory, 2nd Edition. Academic Press. 1989, 309 pp., $44.95. - J. C. Morgan II. Point set theory. Marcel Dekker. 1990, 296 pp., $119.50. - M. Pavel. Fundamentals of Pattern Recognition. Marcel Dekker. 1989, 183 pp., $107.50. - J. Roitman. Introduction to Modern Set Theory. Wiley. 1990, 156 pp., £32-15. - C. Rogers and W. F. Ames. Nonlinear Boundary Value Problems in Science and Engineering. Academic Press. 1989, 417 pp., $69.9 - D. E. Rowe and J. Mccleary, Editors. The History of Modern Mathematics. Vol. II: Institutions and Applications. Academic Press. 1989, 325 pp., $37.50. - D. Ruelle. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. 1989, 187 pp., $27.50 - Y. A. Ryzhov, U. G. Pirumov and V. N. Gorbunov. Nonequilibrium condensation in high-speed gas flows. Gordon and Breach. 1989, 290 pp., $199. - Y. G. Sinai, Editor. Dynamical Systems II. Springer. 1989, 281 pp., DM 128. - V. I. Arnold and S. P. Novikov, Editors. Dynamical Systems IV. Springer. 1990, 283 pp., DM 128. - P. Smith and R. C. Smith. Mechanics. 2nd Edition. Wiley. 1990, 316 pp., £13-95. - G. Stépán. Retarded dynamical systems: stability and characteristic functions. Longman. 1989, 151 pp., £16-50. - G. Toth. Harmonic maps and minimal immersions through representation theory. Academic Press. 1990, 154 pp., $24.95. - M. Vaughan-Lee. The restricted Burnside problem. Oxford University Press. 1990, 209 pp., £27-50. - F. Verhulst. Nonlinear Differential Equations and Dynamical Systems. Springer. 1990, 277 pp., DM38. - A. G. Vitushkin, Editor. Several Complex Variables, I. Springer. 1990, 248 pp., DM128. - W. L. Wood. Practical Time-stepping Schemes. Clarendon Press. 1990, 373 pp., £17-50. - H. S. Wilf. Generating functionology. Academic Press. 1990, 184 pp., $29.95. - M. Young. The Technical Writer's Handbook. Oxford University Press. 1989, 232 pp., £14-95. - E. Zauderer. Partial Differential Equations of Applied Mathematics, 2nd Edition. Wiley. 1989, 891 pp., £51.30 hardback, £29.75 paperback.
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 07 April 2017, pp. 332-340
- Print publication:
- December 1990
-
- Article
- Export citation
On the union of convex bodies with no interior point in common
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-250
- Print publication:
- December 1990
-
- Article
- Export citation
Sums of powers of the zeros of the Bessel polynomials
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-315
- Print publication:
- December 1990
-
- Article
- Export citation
Small zeros of quadratic congruences modulo pq
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 261-272
- Print publication:
- December 1990
-
- Article
- Export citation
On the lower bound sieve
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-286
- Print publication:
- December 1990
-
- Article
- Export citation
Görtler vortices in growing boundary layers: The leading edge receptivity problem, linear growth and the nonlinear breakdown stage
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-189
- Print publication:
- December 1990
-
- Article
- Export citation
Index to volume 37
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, p. 341
- Print publication:
- December 1990
-
- Article
- Export citation
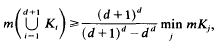
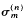 be the sum of the
be the sum of the 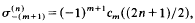
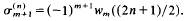
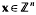 such that
such that
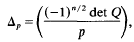
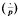 is the Legendre symbol.
is the Legendre symbol.