Refine search
Actions for selected content:
9012 results in Discrete Mathematics, Information Theory and Coding
On p-Class Groups of Cyclic Extensions of Prime Degree p of Quadratic Fields
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-102
- Print publication:
- June 1989
-
- Article
- Export citation
The viscous flow through symmetric collapsible channels
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-181
- Print publication:
- June 1989
-
- Article
- Export citation
On -complete filters
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-115
- Print publication:
- June 1989
-
- Article
- Export citation
On inductive limits of measure spaces and projective limits of Lp-spaces
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-130
- Print publication:
- June 1989
-
- Article
- Export citation
Tangential Limits for Certain Classes of Analytic Functions
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-49
- Print publication:
- June 1989
-
- Article
- Export citation
An analytical bound on the asymmetry of a section of a typical three-dimensional brownian path
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-106
- Print publication:
- June 1989
-
- Article
- Export citation
Illuminating sets of constant width
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 180-189
- Print publication:
- December 1988
-
- Article
- Export citation
The two-ball property: transitivity and examples
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-197
- Print publication:
- December 1988
-
- Article
- Export citation
The magnetic field perturbations produced by an ellipsoidal cavity in a uniform conductor
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-255
- Print publication:
- December 1988
-
- Article
- Export citation
Tauberian theorems for Jakimovski and Karamata-Stirling methods
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-224
- Print publication:
- December 1988
-
- Article
- Export citation
A generalization of mixed invariant sets
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-206
- Print publication:
- December 1988
-
- Article
- Export citation
Systems of parameters for non-finitely generated modules and big Cohen–Macaulay modules
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-215
- Print publication:
- December 1988
-
- Article
- Export citation
Distribution of rational points on varieties over finite fields
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-171
- Print publication:
- December 1988
-
- Article
- Export citation
Convex bodies, economic cap coverings, random polytopes
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-291
- Print publication:
- December 1988
-
- Article
- Export citation
Asymptotic theory for third-order differential equations
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-232
- Print publication:
- December 1988
-
- Article
- Export citation
The exact length of the Euclidean algorithm in
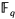 [X]
[X]
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 297-304
- Print publication:
- December 1988
-
- Article
- Export citation
Index to Volume 35
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, p. 309
- Print publication:
- December 1988
-
- Article
- Export citation
MTK volume 35 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
On packings and coverings of unit density
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-179
- Print publication:
- December 1988
-
- Article
- Export citation
The fractional parts of a smooth sequence
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 292-296
- Print publication:
- December 1988
-
- Article
- Export citation
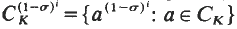 for
for 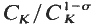 is an elementary abelian
is an elementary abelian 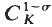 . We let
. We let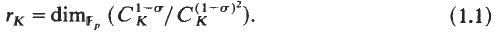
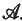 , ) is the inductive limit of the measure spaces (
, ) is the inductive limit of the measure spaces (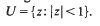
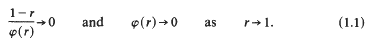
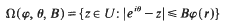
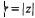 The region . makes tangential contact with the boundary
The region . makes tangential contact with the boundary 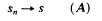
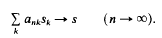
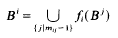
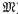 ) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated
) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated 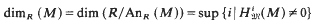
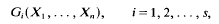
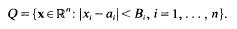
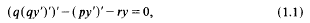
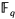 [
[