Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
3 - Examples and growth rates
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 49-80
-
- Chapter
- Export citation
5 - Miscellaneous topics
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 117-144
-
- Chapter
- Export citation
2 - Preliminaries
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 19-48
-
- Chapter
- Export citation
Contents
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp vii-viii
-
- Chapter
- Export citation
4 - Subgroups
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 81-116
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp i-vi
-
- Chapter
- Export citation
Index
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 155-160
-
- Chapter
- Export citation
1 - Background
-
- Book:
- Oligomorphic Permutation Groups
- Published online:
- 23 November 2009
- Print publication:
- 29 June 1990, pp 1-18
-
- Chapter
- Export citation
A new notion of κ-Souslin operation
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 9-20
- Print publication:
- June 1990
-
- Article
- Export citation
Surfaces with congruent shadow-lines
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-58
- Print publication:
- June 1990
-
- Article
- Export citation
On Eggleston's theorem about affine diameters
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-84
- Print publication:
- June 1990
-
- Article
- Export citation
Chapter 9 - Map Coloring
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 125-135
-
- Chapter
- Export citation
Glossary
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 148-150
-
- Chapter
- Export citation
Chapter 3 - Trees
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 37-52
-
- Chapter
- Export citation
Introduction
-
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 3-4
-
- Chapter
- Export citation
Chapter 1 - What Is a Graph?
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 5-23
-
- Chapter
- Export citation
Contents
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp vii-viii
-
- Chapter
- Export citation
On simultaneous additive equations, III
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-96
- Print publication:
- June 1990
-
- Article
- Export citation
Chapter 2 - Connected Graphs
-
- Book:
- Graphs and Their Uses
- Published by:
- Mathematical Association of America
- Published online:
- 05 January 2012
- Print publication:
- 01 June 1990, pp 24-36
-
- Chapter
- Export citation
Diophantine approximation and a lower bound for Hausdorff dimension
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 59-73
- Print publication:
- June 1990
-
- Article
- Export citation
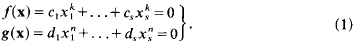
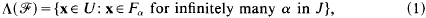
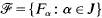 is a family of subsets of
is a family of subsets of 