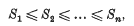Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
MTK volume 2 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1955
-
- Article
-
- You have access
- Export citation
Representation of integers by indefinite quadratic forms
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-38
- Print publication:
- June 1955
-
- Article
- Export citation
An elementary proof of Kato's lemma
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-41
- Print publication:
- June 1955
-
- Article
- Export citation
Witt groups and hyperexponential groups
-
- Journal:
- Mathematika / Volume 2 / Issue 1 / June 1955
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-31
- Print publication:
- June 1955
-
- Article
- Export citation
The Minkowski-Hlawka theorem
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-124
- Print publication:
- June 1954
-
- Article
- Export citation
On the steady motion of viscous liquid past a flat plate
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-156
- Print publication:
- June 1954
-
- Article
- Export citation
A two dimensional magnetic boundary layer problem
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-142
- Print publication:
- June 1954
-
- Article
- Export citation
Partial well-ordering of sets of vectors
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-95
- Print publication:
- June 1954
-
- Article
- Export citation
MTK volume 1 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1954
-
- Article
-
- You have access
- Export citation
A note on Stokes's stream-function for the slow steady motion of viscous fluid before plane and spherical boundaries
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-130
- Print publication:
- June 1954
-
- Article
- Export citation
On irregularities of distribution
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-79
- Print publication:
- June 1954
-
- Article
- Export citation
The representation of integers by positive ternary quadratic forms
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-110
- Print publication:
- June 1954
-
- Article
- Export citation
The triangle as a geometric variable
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-88
- Print publication:
- June 1954
-
- Article
- Export citation
Torsion of cylinders with inclusions*
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-103
- Print publication:
- June 1954
-
- Article
- Export citation
Index to volume 1
-
- Journal:
- Mathematika / Volume 1 / Issue 2 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 157
- Print publication:
- June 1954
-
- Article
- Export citation
A simple proof of η(— 1/τ)= η(τ)√τ/i
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, p. 4
- Print publication:
- June 1954
-
- Article
- Export citation
Simultaneous Diophantine Approximation
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-72
- Print publication:
- June 1954
-
- Article
- Export citation
On convergence and summability factors in a sequence
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-44
- Print publication:
- June 1954
-
- Article
- Export citation
History of Science and Psychology of Invention
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
- Print publication:
- June 1954
-
- Article
- Export citation
The minimal points of a positive definite quadratic form
-
- Journal:
- Mathematika / Volume 1 / Issue 1 / June 1954
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-17
- Print publication:
- June 1954
-
- Article
- Export citation
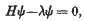
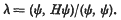
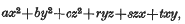
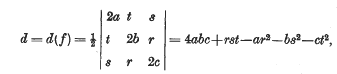
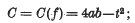
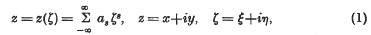
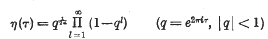
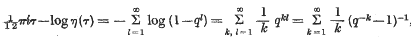
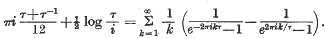
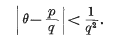

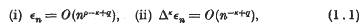
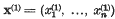 be a point at which this value is attained. Let
be a point at which this value is attained. Let