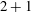Refine search
Actions for selected content:
8125 results in Fluid dynamics and solid mechanics
8 - Post-processing
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 319-336
-
- Chapter
- Export citation
4 - Melt- and solution blowing
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 89-178
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 1-24
-
- Chapter
- Export citation
2 - Polymer physics and rheology
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 25-62
-
- Chapter
- Export citation
11 - Applications of micro- and nanofibers, and micro- and nanoparticles: healthcare, nutrition, drug delivery and personal care
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 380-431
-
- Chapter
- Export citation
3 - General quasi-one-dimensional equations of dynamics of free liquid jets, capillary and bending instability
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 63-88
-
- Chapter
- Export citation
9 - Applications of micro- and nanofibers
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 337-358
-
- Chapter
- Export citation
10 - Military applications of micro- and nanofibers
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 359-379
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp i-iv
-
- Chapter
- Export citation
Preface
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp ix-xii
-
- Chapter
- Export citation
7 - Tensile properties of micro- and nanofibers
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp 297-318
-
- Chapter
- Export citation
Contents
-
- Book:
- Fundamentals and Applications of Micro- and Nanofibers
- Published online:
- 05 June 2014
- Print publication:
- 08 May 2014, pp v-viii
-
- Chapter
- Export citation

Waves and Mean Flows
-
- Published online:
- 05 April 2014
- Print publication:
- 06 March 2014
THREE-DIMENSIONAL WAVE-FREE POTENTIALS IN THE THEORY OF WATER WAVES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 175-195
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 2 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. b1-b11
-
- Article
-
- You have access
- Export citation
AN OPTIMAL DIVIDEND POLICY WITH DELAYED CAPITAL INJECTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 129-150
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 2 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
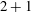 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
BIASED RANDOM WALKS, PARTIAL DIFFERENTIAL EQUATIONS AND UPDATE SCHEMES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 93-108
-
- Article
-
- You have access
- Export citation
A CARTOPT METHOD FOR BOUND-CONSTRAINED GLOBAL OPTIMIZATION
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 109-128
-
- Article
-
- You have access
- Export citation